In diesem Artikel stelle ich verschiedene Beispiele für Regression in R bereit. Ich vergleiche verschiedene Regressionsmethoden mit R. Die Methoden, die ich vorstellen werde, sind einfache lineare Regression, multiple lineare Regression, Polynomregression, Entscheidungsbaumregression und Support-Vektor-Maschinenregression.
Erforderliche Pakete für die Regression in R
Ich beginne damit, die erforderlichen Pakete zu laden (zusätzlich zur R-Basisbibliothek):
library(dplyr) # package for data wranglinglibrary(ggplot2) # package for data visualization
library(rpart) # package for decision tree regression analysis
library(randomForest) # package for random forest regression analysislibrary(e1071) # package for support vector regression analysis
library(caTools) # package for e.g. splitting into training and test setsEinlesen der Daten vor der Regression in R
Ich lese nun Daten ein, die ich für die Umsetzung meiner Regressionsbeispiele in R verwenden werde. Die Daten enthalten Daten zum Bruttoinlandsprodukt, den privaten Bruttoinvestitionen, der Lebenserwartung, der Bevölkerungsgröße und den Investitionen in Forschung und Entwicklung.
# reading in gross domestic product data
gdp_df <- read.csv("gross domestic product.csv",header=TRUE)
# reading in gross private investment data
investment_df <- read.csv("gross private investments.csv",header=TRUE)
# reading in life expectancy data
lifeexpectancy_df <- read.csv("life expectancy.csv",header=TRUE)
# reading in population data
population_df <- read.csv("population.csv",header=TRUE)
# reading in research and development data
rnd_df <- read.csv("research and development.csv",header=TRUE)
# joining all data into a final input data set
data_df <- gdp_df %>% inner_join(investment_df,by="DATE",fa) %>%
inner_join(lifeexpectancy_df,by="DATE") %>%
inner_join(population_df,by="DATE") %>%
inner_join(rnd_df,by="DATE")
# rename column headers
colnames(data_df) <-c("date",
"gdp",
"private_investment",
"life_expectancy",
"population",
"rnd")
# convert date entries from characters into date data types
data_df$date <- as.Date(data_df$date)Als ersten Schritt möchte ich die Daten visualisieren. Um einen besseren visuellen Vergleich von Wachstumstrends in den Daten zu ermöglichen, normalisiere ich sie. Dazu definiere ich eine Funktion:
normalize_data <- function(x){
return ((x-min(x))/(max(x)-min(x)))
}Mit der Funktion konvertiere ich mein data_df in einen ggplot-freundlichen Datenrahmen, der normalisiert ist. Ich füttere dies zu ggplot und visualisiere die Daten:
dates <- c(data_df$date,
data_df$date,
data_df$date,
data_df$date,
data_df$date)
values <- c(normalize_data(data_df$gdp),
normalize_data(data_df$private_investment),
normalize_data(data_df$life_expectancy),
normalize_data(data_df$population),
normalize_data(data_df$rnd))
sources <- c(rep("gdp",times=nrow(data_df)),
rep("private_investment",times=nrow(data_df)),
rep("life_expectancy",times=nrow(data_df)),
rep("population",times=nrow(data_df)),
rep("rnd",times=nrow(data_df)))
# build ggplot-friendly data frame
ggdata_df <- as.data.frame(matrix(nrow=5*nrow(data_df),ncol=3))
colnames(ggdata_df) <- c("date","value","source")
# populating the ggplot-friendly data frame
ggdata_df$date <- as.Date(dates)
ggdata_df$value <- as.numeric(values)
ggdata_df$source <- sources
# visualize the normalized values (i.e. data set) with ggplot
ggplot(ggdata_df) +
geom_point(mapping = aes(x=dates,y=values,color=sources)) +
ggtitle("Normalized data set values; time-series view") +
xlab("Time") +
ylab("Normalized observation values")
Pipeline für die Regression in r
Nachdem ich den interessierenden Datensatz visualisiert habe, teste ich verschiedene Regressionsmodelle an den Daten.
Für jeden alternativen Ansatz zur Regression in R ist der Prozess immer gleich:
- Daten in Trainings- und Testsatz aufteilen
- Trainieren Sie einen Prädiktor auf dem Trainingsdatensatz
- Überprüfen Sie die Anpassungsgüte für den Regressor basierend auf dem Trainingssatz
- Regressor auf Testmenge testen
Einfache lineare Regression in R
Ich werde meine Beispielserie zur Regression in R mit einem einfachen linearen Regressionsmodell beginnen. Ich versuche, die Bevölkerungsgröße aus den anderen Beobachtungsdaten des Datensatzes vorherzusagen.
Unten implementiere ich die oben erwähnte Pipeline (beachte, dass ich die Daten in diesem Fall nicht normalisieren muss).
Da die Populationsgröße als abhängige Variable dient, stehen mir nun vier unabhängige Variablen zur Auswahl. Für dieses Beispiel wähle ich die Lebenserwartung (bei der Geburt) als vorhersagende unabhängige Variable. Das heißt, für mein Beispiel zur Regression in RI wird in diesem Fall die lineare Beziehung zwischen Bevölkerungsgröße und Lebenserwartung abgeleitet.
Meine Annahme ist, dass eine höhere Lebenserwartung mit einer höheren Bevölkerungszahl einhergeht (für dasselbe Land und dieselbe Region).
# randomly generate split
set.seed(123)
training_split <- sample.split(data_df$date,SplitRatio = 0.8)
# extract training and test sets
training_df <- subset(data_df, training_split)
test_df <- subset(data_df, !training_split)
# train predictor based on training set
predictor <- lm(formula = population ~ life_expectancy, data=training_df)
# print summary of simple linear regression
summary(predictor)##
## Call:
## lm(formula = population ~ life_expectancy, data = training_df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -15279 -6746 1131 4625 17762
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -840396.8 32055.5 -26.22 <2e-16 ***
## life_expectancy 14629.9 427.4 34.23 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 8377 on 44 degrees of freedom
## Multiple R-squared: 0.9638, Adjusted R-squared: 0.963
## F-statistic: 1172 on 1 and 44 DF, p-value: < 2.2e-16Ich visualisiere das Ergebnis dieser Regression in R mit ggplot2. Im folgenden Code zeige ich, wie das geht:
ggplot(training_df) +
geom_point(mapping=aes(x=life_expectancy,
y=population)) +
geom_line(mapping=aes(x=life_expectancy,
y=predict(predictor,training_df)),color="red") +
ggtitle("Population in dependence of life expectancy; linear regression (training)") +
xlab("US life expectancy since birth [years]") +
ylab("US population size [-]")
Ich möchte auch ein Histogramm der Vorhersageresiduen sehen:
hist(predictor$residuals,
main ="Histogram of model residuals",
xlab="Model residuals [-]")
Außerdem möchte ich die Residuen in Abhängigkeit von der Vorhersage der variablen Beobachtungsgröße sehen:
plot(x=training_df$life_expectancy,
y=predictor$residuals,
main = "Model residuals in dependence of independent variable",
xlab="US life expectancy [years]",
ylab="Model residuals [-]")
Dies sieht nach einer etwas systematischen Verzerrung aus. Ich kann auch versuchen, dies in einem qqnorm-Plot zu zeigen:
qqnorm(predictor$residuals)
Nachdem ich den linearen Prädiktor trainiert habe, teste ich die Vorhersageleistung auf dem Testsatz:
# predict the test set values
predictions <- predict(predictor,test_df)
# visualize prediction accuracy
ggplot(test_df) +
geom_point(mapping=aes(x=life_expectancy,y=population)) +
geom_line(mapping=aes(x=life_expectancy,predictions),color="red") +
ggtitle("Population in dependence of life expectancy; linear regression (test)") +
xlab("US life expectancy since birth [years]") +
ylab("US population size [-]")
Mal sehen, ob wir mit einem multivariaten linearen Regressionsansatz genauere Vorhersagen erhalten können. Aber zuerst speichern wir die einfachen Vorhersagen der linearen Regression für den gesamten Datensatz in einem Vektor:
predictions_slr <- predict(predictor,data_df)Mehrfache lineare Regression
Dieses Mal beginne ich damit, alle Variablen im Datensatz zu berücksichtigen, wenn ich die Größe der US-Bevölkerung vorhersehe:
# split data in training and test set
set.seed(123)
training_split <- sample.split(data_df$date, SplitRatio = 0.8)
training_df <- subset(data_df, training_split)
test_df <- subset(data_df, !training_split)
# train predictor with mutliple linear regression methodology, on training set
predictor <- lm(formula = population ~ gdp +
private_investment +
life_expectancy +
rnd, training_df)
# summarize regression outcome
summary(predictor)##
## Call:
## lm(formula = population ~ gdp + private_investment + life_expectancy +
## rnd, data = training_df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -10472.0 -1969.0 188.3 2421.8 7782.1
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -3.202e+05 4.488e+04 -7.133 1.07e-08 ***
## gdp 9.891e+00 2.970e+00 3.330 0.00184 **
## private_investment -3.272e+00 5.115e+00 -0.640 0.52598
## life_expectancy 7.283e+03 6.318e+02 11.527 1.93e-14 ***
## rnd -1.923e+02 8.065e+01 -2.385 0.02181 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3834 on 41 degrees of freedom
## Multiple R-squared: 0.9929, Adjusted R-squared: 0.9922
## F-statistic: 1440 on 4 and 41 DF, p-value: < 2.2e-16Das angepasste R-Quadrat hat sich im Vergleich zur vorherigen einfachen linearen Regression verbessert. Das private Investitionsvolumen scheint für die Vorhersage der US-Bevölkerungsgröße nicht so signifikant zu sein. Daher wende ich eine schrittweise Parameterelimination an, bei der ich das private Investitionsvolumen als unabhängige Variable bei der Durchführung einer Regressionsanalyse eliminiere:
# regression without private investment volume as independent variable
predictor <- lm(formula=population~gdp +
life_expectancy +
rnd, training_df)
# review model performance
summary(predictor)##
## Call:
## lm(formula = population ~ gdp + life_expectancy + rnd, data = training_df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -10412.6 -2275.0 247.7 2209.6 7794.9
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -3.225e+05 4.442e+04 -7.259 6.20e-09 ***
## gdp 8.598e+00 2.160e+00 3.980 0.000267 ***
## life_expectancy 7.316e+03 6.252e+02 11.702 8.41e-15 ***
## rnd -1.673e+02 7.006e+01 -2.388 0.021496 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3807 on 42 degrees of freedom
## Multiple R-squared: 0.9929, Adjusted R-squared: 0.9924
## F-statistic: 1948 on 3 and 42 DF, p-value: < 2.2e-16Der Wegfall des privaten Investitionsvolumens hat das bereinigte R-Quadrat (leicht) verbessert. Ich bin jedoch immer noch daran interessiert, die Verteilung der Residuen zu sehen.
Zuerst ein Histogramm der Residuen:
hist(predictor$residuals)
Als nächstes ein qqnorm-Diagramm der Residuen:
qqnorm(predictor$residuals)
Ich bewerte jetzt die Modellleistung, indem ich die Werte der Testsatzpopulation vorhersehe:
# predict test set population values
predictions <- predict(predictor,test_df)
# visualize model performance vs test set, along timeline
ggplot(test_df) +
geom_point(mapping=aes(x=date,y=population)) +
geom_line(mapping=aes(x=date,y=predictions),color="red") +
ggtitle("Multiple linear regression prediction of US population") +
xlab("Date") +
ylab("US population size [-]")
Bevor ich mit der Polynomregression fortfahre, speichere ich Vorhersagen für den gesamten Datensatz in einem Vektor:
predictions_mlr <- predict(predictor,data_df)Polynomiale Regression in R
In Anbetracht des Ergebnisses der multiplen linearen Regression nach der Rückwärtseliminierung scheint es, dass die Lebenserwartung bei der Vorhersage der Bevölkerungsgröße doch recht hilfreich ist.
Daher versuche ich, eine Polynomregression in R durchzuführen und die Größe der US-Bevölkerung mit Kenntnis der US-Lebenserwartung bei der Geburt vorherzusagen.
Mein Ansatz besteht darin, Polynomterme hinzuzufügen, solange dies das angepasste R-Quadrat verbessert:
# split in training and test set
set.seed(123)
training_split <- sample.split(data_df$date,SplitRatio = 0.8)
training_df <- subset(data_df, training_split)
test_df <- subset(data_df, !training_split)
# train predictor on first order term only, i.e. simple linear regression
predictor <- lm(formula = population ~ life_expectancy,training_df)
# review model performance
summary(predictor)##
## Call:
## lm(formula = population ~ life_expectancy, data = training_df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -15279 -6746 1131 4625 17762
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -840396.8 32055.5 -26.22 <2e-16 ***
## life_expectancy 14629.9 427.4 34.23 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 8377 on 44 degrees of freedom
## Multiple R-squared: 0.9638, Adjusted R-squared: 0.963
## F-statistic: 1172 on 1 and 44 DF, p-value: < 2.2e-16Ich frage mich nun: Kann ich das bereinigte R-Quadrat verbessern, indem ich einen Polynomterm zweiten Grades hinzufüge? Lass mich das testen:
# polynomial two term regression
training_df$LE2 <- training_df$life_expectancy^2
predictor <- lm(formula = population ~ life_expectancy + LE2, training_df)
# review model performance
summary(predictor)##
## Call:
## lm(formula = population ~ life_expectancy + LE2, data = training_df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -10785.9 -4081.8 -715.1 4186.9 8913.4
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 4014088.8 604959.5 6.635 4.35e-08 ***
## life_expectancy -116186.0 16295.0 -7.130 8.34e-09 ***
## LE2 879.9 109.6 8.029 4.31e-10 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 5360 on 43 degrees of freedom
## Multiple R-squared: 0.9855, Adjusted R-squared: 0.9848
## F-statistic: 1463 on 2 and 43 DF, p-value: < 2.2e-16Ja. Das bereinigte R-Quadrat wurde verbessert. Was passiert, wenn ich einen dritten Begriff hinzufüge?
# polynomial three term regression
training_df$LE3 <- training_df$life_expectancy^3
predictor <- lm(formula = population ~ life_expectancy + LE2 + LE3, training_df)
# review model performance
summary(predictor)##
## Call:
## lm(formula = population ~ life_expectancy + LE2 + LE3, data = training_df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -10908 -3739 -862 4079 9125
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.196e+07 2.240e+07 0.534 0.596
## life_expectancy -4.367e+05 9.037e+05 -0.483 0.631
## LE2 5.187e+03 1.214e+04 0.427 0.671
## LE3 -1.927e+01 5.432e+01 -0.355 0.725
##
## Residual standard error: 5415 on 42 degrees of freedom
## Multiple R-squared: 0.9856, Adjusted R-squared: 0.9845
## F-statistic: 955.5 on 3 and 42 DF, p-value: < 2.2e-16Das Hinzufügen eines dritten Terms verbesserte das bereinigte R-Quadrat nicht. Was passiert, wenn ich der Regression in R einen vierten Term hinzufüge?
# polynomial four term regression
training_df$LE4 <- training_df$life_expectancy^4
predictor <- lm(formula = population ~ life_expectancy + LE2 + LE3 + LE4, training_df)
# review model performance
summary(predictor)##
## Call:
## lm(formula = population ~ life_expectancy + LE2 + LE3 + LE4,
## data = training_df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -11422.7 -2990.7 -4.8 2420.7 11496.0
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -2.345e+09 6.041e+08 -3.882 0.000369 ***
## life_expectancy 1.264e+08 3.250e+07 3.889 0.000362 ***
## LE2 -2.553e+06 6.555e+05 -3.895 0.000355 ***
## LE3 2.290e+04 5.873e+03 3.900 0.000350 ***
## LE4 -7.697e+01 1.972e+01 -3.903 0.000346 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 4680 on 41 degrees of freedom
## Multiple R-squared: 0.9895, Adjusted R-squared: 0.9884
## F-statistic: 963.4 on 4 and 41 DF, p-value: < 2.2e-16Das Hinzufügen eines vierten Terms verbesserte die Regression in R, da das angepasste R-Quadrat zunahm. Ich fahre fort, indem ich Terme hinzufüge und einen fünften und sechsten Regressionsterm hinzufüge.
# polynomial six term regression
training_df$LE5 <- training_df$life_expectancy^5
training_df$LE6 <- training_df$life_expectancy^6
predictor <- lm(formula = population ~ life_expectancy + LE2 + LE3 +
LE4 + LE5 + LE6, training_df)
# review model performance
summary(predictor)##
## Call:
## lm(formula = population ~ life_expectancy + LE2 + LE3 + LE4 +
## LE5 + LE6, data = training_df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -12579.2 -2669.2 -306.2 1781.2 12719.2
##
## Coefficients: (1 not defined because of singularities)
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -3.842e+10 1.696e+10 -2.265 0.0290 *
## life_expectancy 2.459e+09 1.097e+09 2.243 0.0305 *
## LE2 -6.145e+07 2.768e+07 -2.220 0.0322 *
## LE3 7.276e+05 3.312e+05 2.197 0.0339 *
## LE4 -3.632e+03 1.671e+03 -2.174 0.0357 *
## LE5 NA NA NA NA
## LE6 4.285e-02 2.013e-02 2.128 0.0395 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 4491 on 40 degrees of freedom
## Multiple R-squared: 0.9905, Adjusted R-squared: 0.9894
## F-statistic: 837.9 on 5 and 40 DF, p-value: < 2.2e-16Das Hinzufügen eines fünften und sechsten Regressionsterms verbesserte das angepasste R-Quadrat. Ich beschließe, weiterzumachen und einen siebten und achten Term hinzuzufügen:
# polynomial seven term regression
training_df$LE7 <- training_df$life_expectancy^7
training_df$LE8 <- training_df$life_expectancy^8
predictor <- lm(formula = population ~ life_expectancy + LE2 + LE3 + LE4 +
LE5 + LE6 + LE7 + LE8, training_df)
# review model performance
summary(predictor)##
## Call:
## lm(formula = population ~ life_expectancy + LE2 + LE3 + LE4 +
## LE5 + LE6 + LE7 + LE8, data = training_df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -12579.2 -2669.2 -306.2 1781.2 12719.2
##
## Coefficients: (3 not defined because of singularities)
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -3.842e+10 1.696e+10 -2.265 0.0290 *
## life_expectancy 2.459e+09 1.097e+09 2.243 0.0305 *
## LE2 -6.145e+07 2.768e+07 -2.220 0.0322 *
## LE3 7.276e+05 3.312e+05 2.197 0.0339 *
## LE4 -3.632e+03 1.671e+03 -2.174 0.0357 *
## LE5 NA NA NA NA
## LE6 4.285e-02 2.013e-02 2.128 0.0395 *
## LE7 NA NA NA NA
## LE8 NA NA NA NA
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 4491 on 40 degrees of freedom
## Multiple R-squared: 0.9905, Adjusted R-squared: 0.9894
## F-statistic: 837.9 on 5 and 40 DF, p-value: < 2.2e-16Das bereinigte R-Quadrat verbesserte sich nicht . Ich beschließe, die Polynomregression hier zu stoppen und das Ergebnis der Regression zu visualisieren:
ggplot(training_df) +
geom_point(mapping=aes(x=life_expectancy,y=population)) +
geom_line(mapping=aes(x=life_expectancy,y=predict(predictor,training_df)),
color="red") +
ggtitle("Trained polynomial regression model; degree 6") +
xlab("US life expectancy at birth [years]") +
ylab("US population size [-]")
Jetzt teste ich das Polynommodell gegen die Testmenge:
# add terms to test data frame
test_df$LE2 <- test_df$life_expectancy^2
test_df$LE3 <- test_df$life_expectancy^3
test_df$LE4 <- test_df$life_expectancy^4
test_df$LE5 <- test_df$life_expectancy^5
test_df$LE6 <- test_df$life_expectancy^6
test_df$LE7 <- test_df$life_expectancy^7
test_df$LE8 <- test_df$life_expectancy^8
# visualize predictor performance on test set
predictions <- predict(predictor,test_df)
ggplot(test_df) +
geom_point(mapping=aes(x=life_expectancy,y=population)) +
geom_line(mapping=aes(x=life_expectancy,y=predictions), color = "red") +
ggtitle("Polynomial regression on test data; degree 6") +
xlab("US life expectancy at birth [years]") +
ylab("US population size [-]")
Bevor ich zur Entscheidungsbaumregression übergehe, speichere ich Vorhersagen für den gesamten Datensatz in einem Vektor:
data_df$LE2 <- data_df$life_expectancy^2
data_df$LE3 <- data_df$life_expectancy^3
data_df$LE4 <- data_df$life_expectancy^4
data_df$LE5 <- data_df$life_expectancy^5
data_df$LE6 <- data_df$life_expectancy^6
data_df$LE7 <- data_df$life_expectancy^7
data_df$LE8 <- data_df$life_expectancy^8
predictions_poly <- predict(predictor,data_df)Entscheidungsbaumregression in R
Eine weitere Regressionsmethode ist die Entscheidungsbaumregression. Bei dieser Art der Regression wird der Lösungsraum in Teilmengen aufgeteilt, für die der im Trainingssatz gemessene durchschnittliche Beobachtungswert eine Vorhersage darstellt.
Im folgenden Abschnitt implementiere ich die Entscheidungsbaumregression in R:
# split in training and test set
set.seed(123)
training_split <- sample.split(data_df$date,SplitRatio = 0.8)
training_df <- subset(data_df, training_split)
test_df <- subset(data_df, !training_split)
# conduct decision tree regression
predictor <- rpart(formula = population ~ gdp +
private_investment +
life_expectancy +
population +
rnd,
data = training_df)
# generate predictions from test set
predictions <- predict(predictor,test_df)
residuals <- test_df$population - predictions
# visualize prediction accuracy along the timeline
ggplot(test_df) +
geom_point(mapping = aes(x=date,y=population)) +
geom_point(mapping = aes(x=date,y=predictions), color = "red") +
ggtitle("Decision tree regression performance on test set (red: predictions)") +
xlab("Date") +
ylab("US population size [-]")
Bevor ich zur Unterstützung der Vektorregression übergehe, speichere ich meine Vorhersagen für den gesamten Datensatz in einem anderen Vektor:
predictions_dtr <- predict(predictor,data_df)Vektorregression unterstützen
Schließlich führe ich eine Support-Vektor-Regression durch. Ich füttere nur die Variablen, die sich in der multiplen linearen Regression als statistisch signifikant für die Vorhersage der US-Bevölkerungsgröße erwiesen haben:
# split in training and test set
set.seed(123)
training_split <- sample.split(data_df$date,SplitRatio = 0.8)
training_df <- subset(data_df, training_split)
test_df <- subset(data_df, !training_split)
# construct predictor
predictor <- svm(formula = population ~ gdp +
life_expectancy +
rnd,
data = training_df,
type = "eps-regression")
# visualize prediction accuracy on test set along time line
ggplot(test_df) +
geom_point(mapping = aes(x=date, y = population)) +
geom_line(mapping = aes(x=date, y = predict(predictor,test_df)), color = "red") +
ggtitle("Support vector regression (eps methode) on test set") +
xlab("Date") +
ylab("US population size [-]")
Wie in den anderen Regressionsteilen speichere ich die Vorhersage über den gesamten Datensatz als Lösungsraum in einem separaten Vektor:
predictions_svr <- predict(predictor,data_df)Vergleich von Modellvorhersagen
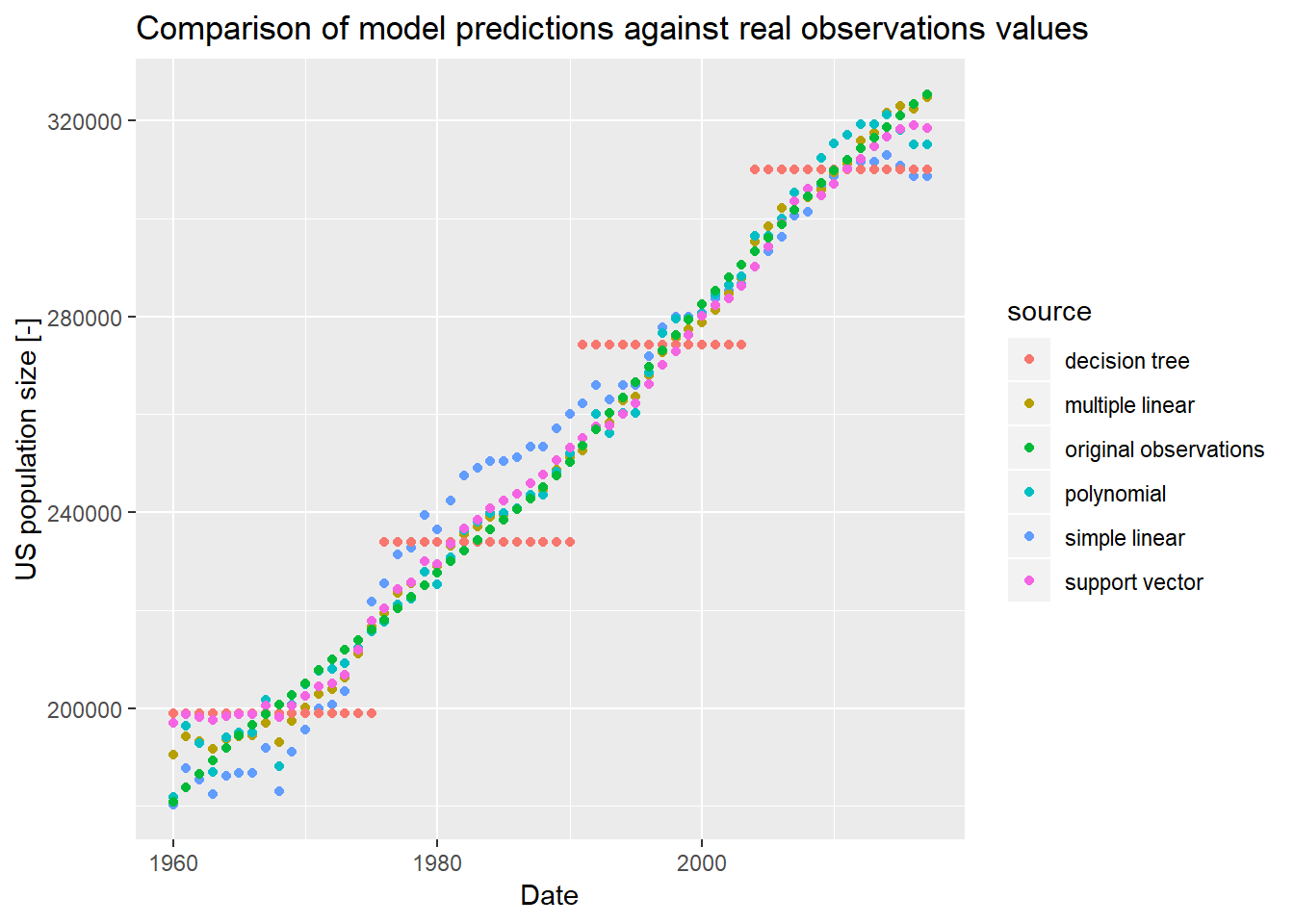
Anhand der Vektoren mit gespeicherten Vorhersagewerten können wir die verschiedenen Vorhersagemodelle über die Zeitachse hinweg vergleichen:
# construct ggplot friendly data frame
ggdata_df <- as.data.frame(matrix(nrow=nrow(data_df)*6,ncol=3))
colnames(ggdata_df) <- c("date","value","source")
ggdata_df$date <- rep(data_df$date,times=6)
ggdata_df$value <- c(predictions_slr,
predictions_mlr,
predictions_poly,
predictions_dtr,
predictions_svr,
data_df$population)
ggdata_df$source <- c(rep("simple linear", times=nrow(data_df)),
rep("multiple linear", times=nrow(data_df)),
rep("polynomial", times=nrow(data_df)),
rep("decision tree", times=nrow(data_df)),
rep("support vector", times=nrow(data_df)),
rep("original observations", times=nrow(data_df)))
# visualize
ggplot(ggdata_df) +
geom_point(mapping = aes(x=date, y=value, color=source)) +
ggtitle("Comparison of model predictions against real observations values") +
xlab("Date") +
ylab("US population size [-]")

Wirtschaftsingenieur mit Interesse an Optimierung, Simulation und mathematischer Modellierung in R, SQL, VBA und Python

Leave a Reply