In einem früheren Beitrag habe ich gezeigt, wie ein 2D-Gitter mit Matplotlib und Pyplot in Python visualisiert werde kann (Beitrag mit dem Titel „Visualisierung von 2D-Gittern mit Matplotlib in Python“). Dieser Beitrag war als erste Einführung in die Visualisierung von Gittern in Python gedacht. Das Visualisieren von Gittern kann von Interesse sein wenn z.B. Ergebnisse agentenbasierter Simulationsstudien dargestellt werden sollen.
In diesem Beitrag modelliere ich die Grundlagen eines einfachen agentenbasierten Simulationsmodells unter Verwendung einer 2D-List als Gitter-Umgebung welche von zwei Arten von Agenten gefüllt werden kann.
Dieses 2D-Gitter dient als Schlachtfeld auf dem zwei Gruppen von Agenten eine Schlacht führen.
Agenten haben die gleichen Attribute, eines davon ist ihre Gruppenmitgliedschaft. Außerdem haben sie alle eine Lebensbewertung die zu Beginn der Simulation für alle Agenten gleich ist. Schließlich haben sie einen Satz an Koordinaten (x- und y-Koordinaten) um ihre räumliche Position in einer zweidimensionalen Welt darstellen zu können.
Ich werde in diesem Beitrag keine Simulationsstudie durchführen. Dies wird in einem kommenden Beitrag geschehen. Ich werde das Modell aus diesem Beitrag in zukünftigen Beiträgen verwenden, um einen Kampf zwischen den beiden Gruppen von Agenten zu simulieren.
Im folgenden Codefragment definiere ich eine Klasse für Agente. Die Klase enthält relevante Attribute und Methoden zur abstrakten Darstellung von Agenten. Die Dokumentation wird dem Code in Form von Kommentaren hinzugefügt.
# Klasse, die Agenten als abstrakte Datentypen definiert
class agent:
# init-method, die Konstruktormethode für Agenten
def __init__(self,x,y,group):
self.life = 100.0 # agent's life score
self.x = x
self.y = y
self.group = groupDer nächste Schritt besteht darin ein 2D-Gitter in Form einer 2D-Liste zu definieren. Zeilen stehen für x-Koordinaten, Spalten für y-Koordinaten. Diese 2D-Liste repräsentiert das Schlachtfeld. Ich definiere es so, dass es eine Größe von 100 x 100 Zellen hat, d. H. 10.000 Stellen. Ich werde den Standardlistentyp in Python verwenden, um dieses „Schlachtfeld“ -Array zu definieren. Der richtige Weg ist die Verwendung von List-Comprehensions in Python:
# Erstellen einer leeren 100 x 100-Liste mithilfe des Listenverständnisses in Python battlefield = [[None for i in range(0,100)] for i in range(0,100)]
Als Nächstes werde ich zwei Agentengruppen erstellen und sie an zufälligen Koordinaten auf dem Schlachtfeld platzieren. In separaten Listen speichere ich außerdem Verweise auf die Agentenobjekte. Ich werde 1000 Agenten der Gruppe A und 1000 Agenten der Gruppe B erstellen.
# Liste mit verfügbaren x- und y-Positionen
locations = battlefield.copy() # using .copy prevents copying by reference
# Erstellen Sie eine leere Liste für zukünftige Agentenreferenzen. Geben Sie A & B ein
agents_A = []
agents_B = []
# Zuweisen von zufälligen Stellen zu Agenten der Gruppen A und B;
# - dafür brauche ich das Zufallsmodul, also importiere es
import random
# - Definiere eine Funktion zum Erstellen und Zuweisen von Agenten zum Raster
def agentCreator(size,group,groupList,field,n,m):
# Schleife durch die gesamte Gruppe, d. h. in diesem Fall 1000 Einheiten
for j in range(0,size):
# Wählen Sie einen zufällig verfügbaren Ort aus
while True:
# zufällige x-Koordinate
x = random.choice(range(0,n))
# zufällige y-Koordinate
y = random.choice(range(0,m))
# prüfen, ob Platz frei ist; Wenn nicht, wiederhole den Vorgang
if field[x][y] == None:
field[x][y] = agent(x=x,y=y,group=group)
# Agentenobjektreferenz an Gruppenliste anhängen
groupList.append(field[x][y])
# verlasse while-Schleife; Punkt auf dem Feld wird genommen
break
# - Ich bevölkere das Schlachtfeld mit der Funktion agentCreator
agentCreator(size = 1000,
group = "A",
groupList = agents_A,
field = battlefield,
n = 100,
m = 100)
agentCreator(size = 1000,
group = "B",
groupList = agents_B,
field = battlefield,
n = 100,
m = 100) Das als 2D-Liste dargestellte „Schlachtfeld“ enthält jetzt entweder „nichts“ oder Objektreferenzen für Agenten von entweder Typ A oder B. Alle Agenten haben eine Lebensbewertung von 100 da der Kampf noch nicht begonnen hat.
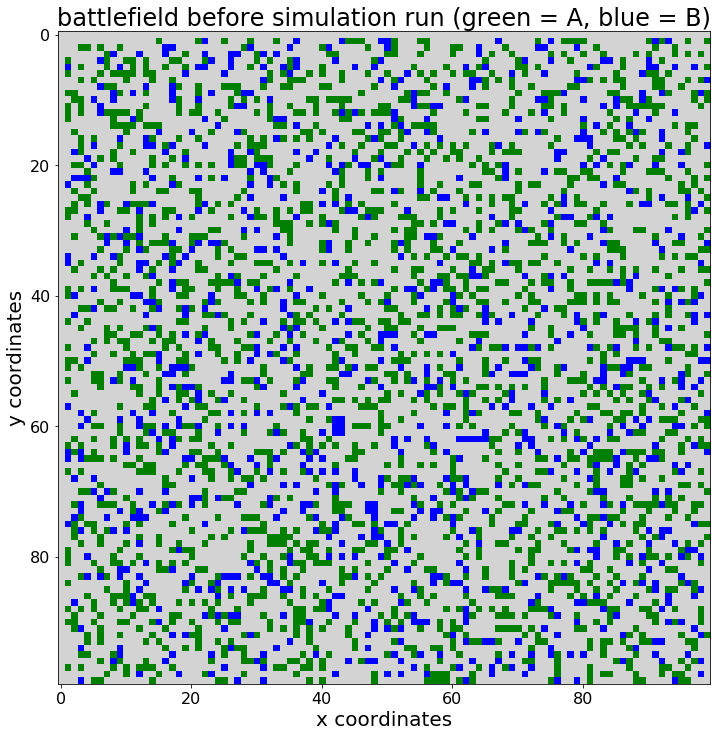
Um diesen ersten Beitrag zu agentenbasierter Simulation abschließen zu können, werde ich den Standort von Agenten vom Typ A und den Standort von Agenten vom Typ B in zwei separaten Rasterplots visualisieren. Der Schlüssel dazu ist die Verwendung von matplotlib.pyplot mit der Methode .imshow ():
# .imshow () benötigt eine Matrix mit float-Elementen;
population = [[0.0 for i in range(0,100)] for i in range(0,100)]
# Wenn der Agent vom Typ A ist, geben Sie eine 1,0 ein, wenn er vom Typ B ist, geben Sie eine 2,0 ein
for i in range(1,100):
for j in range(1,100):
if battlefield[i][j] == None: # empty
pass # 0,0 in der Populationszelle belassen
elif battlefield[i][j].group == "A": # Agenten der Gruppe A.
population[i][j] = 1.0 # 1,0 bedeutet "A"
else: # Agenten der Gruppe B.
population[i][j] = 2.0 # 2,0 bedeutet "B"
# Pyplot und Farben aus matplotlib importieren
from matplotlib import pyplot, colors
# Definieren Sie mithilfe von Farben aus matplotlib eine Farbkarte
colormap = colors.ListedColormap(["lightgrey","green","blue"])
# Definieren Sie die Figurengröße mit Pyplot
pyplot.figure(figsize = (12,12))
# Mit Pyplot einen Titel hinzufügen
pyplot.title("battlefield before simulation run (green = A, blue = B)",
fontsize = 24)
# Fügen Sie mit Pyplot x- und y-Beschriftungen hinzu
pyplot.xlabel("x coordinates", fontsize = 20)
pyplot.ylabel("y coordinates", fontsize = 20)
# Passen Sie die Ticks der x- und y-Achse mithilfe des Pyplots an
pyplot.xticks(fontsize = 16)
pyplot.yticks(fontsize = 16)
# Verwenden Sie die .imshow () -Methode von pyplot, um die Agentenpositionen zu visualisieren
pyplot.imshow(X = population,
cmap = colormap)<matplotlib.image.AxesImage at 0x1c756b04c88>

In einem kommenden Beitrag werde ich das in diesem Beitrag entwickelte Grundmodell verwenden um den tatsächlichen Kampf zwischen den beiden Gruppen zu simulieren. Wir werden verschiedene Parameter untersuchen und so sehen wie diese den Kampfausgang beeinflussen.

Wirtschaftsingenieur mit Interesse an Optimierung, Simulation und mathematischer Modellierung in R, SQL, VBA und Python




Leave a Reply