I nogle af mine indlæg brugte jeg lpSolve eller FuzzyLP i R til at løse lineære optimeringsproblemer. Jeg har også brugt PuLP og SciPy.optimize i Python til at løse sådanne problemer. I alle disse tilfælde havde problemet kun én enkelt objektiv funktion.
I dette indlæg vil jeg give et kodeeksempel i Python ved hjælp af PuLP-modulet til løsning af et multi-objektivt lineært optimeringsproblem.
Et multi-objektivt lineært optimeringsproblem er et lineært optimeringsproblem med flere objektive funktioner, dvs. med flere optimeringskriterier. Dette subområde indenfor lineær programmering kaldes også multi-objektiv lineær programmering eller multi-mål lineær programmering.
Nedenfor viser jeg et eksemplarisk multi-objektivt lineært optimeringsproblem med to objektive funktioner:

Under antagelse af, at de to objektive funktioner repræsenterer to forskellige mål så som f.eks. serviceniveau og gevinst, prøver jeg to alternative tilgange til løsning af dette problem.
Den første tilgang vil være at løse et af målene og derefter løse problemet med det optimale resultat af det første problem ved at tilføje en yderligere begrænsning til det andet optimeringsløb, hvor jeg derefter maksimerer den anden objektive funktion (underlagt begrænsningen af holde den optimale objektive værdi til det første delproblem).
Den anden tilgang vil være at tilføje de to mål sammen, dvs. at slå dem sammen til en objektiv funktion ved at anvende vægte. Ved at prøveprøve vægtene og løse det kombinerede problem for hver prøve, kan det optimale resultat gennemgås afhængigt af vægten.
Fremgangsmåde #1: Maksimering for et mål, derefter tilføjes det som en begrænsning og løsning af det andet mål
Ved hjælp af PuLP maksimerer jeg det første mål først, så tilføjer jeg den objektive funktion som en begrænsning for det oprindelige problem og maksimerer det andet mål med forbehold for alle begrænsninger, herunder den yderligere begrænsning.
I matematisk syntaks kan det problem, vi først løser, angives som følger:

Her er implementeringen af ovenstående problemangivelse i Python ved hjælp af PuLP-modulet:
# først, importer PuLP
import pulp
# udfør derefter den første erklæring om problemet
linearProblem = pulp.LpProblem("Maximizing for first objective",pulp.LpMaximize)
# definer optimeringsvariabler ved hjælp af PuLP
x1 = pulp.LpVariable("x1",lowBound = 0)
x2 = pulp.LpVariable("x2",lowBound = 0)
# tilføj (første) objektive funktion til den lineære problemangivelse
linearProblem += 2*x1 + 3*x2
# tilføj begrænsningerne til problemet
linearProblem += x1 + x2 <= 10
linearProblem += 2*x1 + x2 <= 15
# løse med standardløseren, maksimere det første mål
solution = linearProblem.solve()
# outputinformation, hvis der blev fundet optimalt, hvad den maksimale objektive værdi er, og hvad det optimale punkt er
print(str(pulp.LpStatus[solution])+" ; max value = "+str(pulp.value(linearProblem.objective))+
" ; x1_opt = "+str(pulp.value(x1))+
" ; x2_opt = "+str(pulp.value(x2)))
Optimal ; max value = 30.0 ; x1_opt = 0.0 ; x2_opt = 10.0
Nu modellerer jeg igen det oprindelige problem, således at den anden objektive funktion maksimeres med forbehold af en yderligere begrænsning. Denne yderligere begrænsning anmoder om, at det første mål skal være mindst 30. Ved hjælp af matematisk syntaks kan det problem, jeg nu løser, angives som følger:

Her er implementeringen af ovenstående problemangivelse i Python ved hjælp af PuLP:
# ombyg problemopgørelsen
linearProblem = pulp.LpProblem("Maximize second objective",pulp.LpMaximize)
linearProblem += 4*x1 - 2*x2
linearProblem += x1 + x2 <= 10
linearProblem += 2*x1 + x2 <= 15
linearProblem += 2*x1 + 3*x2 >= 30
# gennemgå problemerklæring efter ombygning
linearProblem
Maximize_second_objective: MAXIMIZE 4*x1 + -2*x2 + 0 SUBJECT TO _C1: x1 + x2 <= 10 _C2: 2 x1 + x2 <= 15 _C3: 2 x1 + 3 x2 >= 30 VARIABLES x1 Continuous x2 Continuous
Nu løser jeg dette problem ved hjælp af standardløseren i PuLP:
# anvend standardløseren
solution = linearProblem.solve()
# output en streng, der opsummerer, om der blev fundet optimalt, og i bekræftende fald hvad den optimale løsning
print(str(pulp.LpStatus[solution])+" ; max value = "+str(pulp.value(linearProblem.objective))+
" ; x1_opt = "+str(pulp.value(x1))+
" ; x2_opt = "+str(pulp.value(x2)))
Optimal ; max value = -19.999999999995993 ; x1_opt = 1.0018653e-12 ; x2_opt = 10.0
Denne tilgang antyder, at x1 = 0 og x2 = 10 er den optimale løsning. De optimale objektive værdier ville være 30 for mål 1 og -20 for mål to.
Fremgangsmåde #2: Kombiner mål ved hjælp af sammenfattende vægte og iterationer med defineret trinstørrelse
Når vi anvender denne tilgang, definerer vi det oprindelige problem som følger:

Spørgsmålet er nu, hvordan man sætter vægtparametren α.
En typisk tilgang i en situation som denne er, at man identificere den effektive grænse. Indenfor teoretisk økonomi er dette f.eks. kendt som “pareto-optimalitet”. Vi leder altså efter løsninger hvor ingen af målværdierne kan forbedres uden at
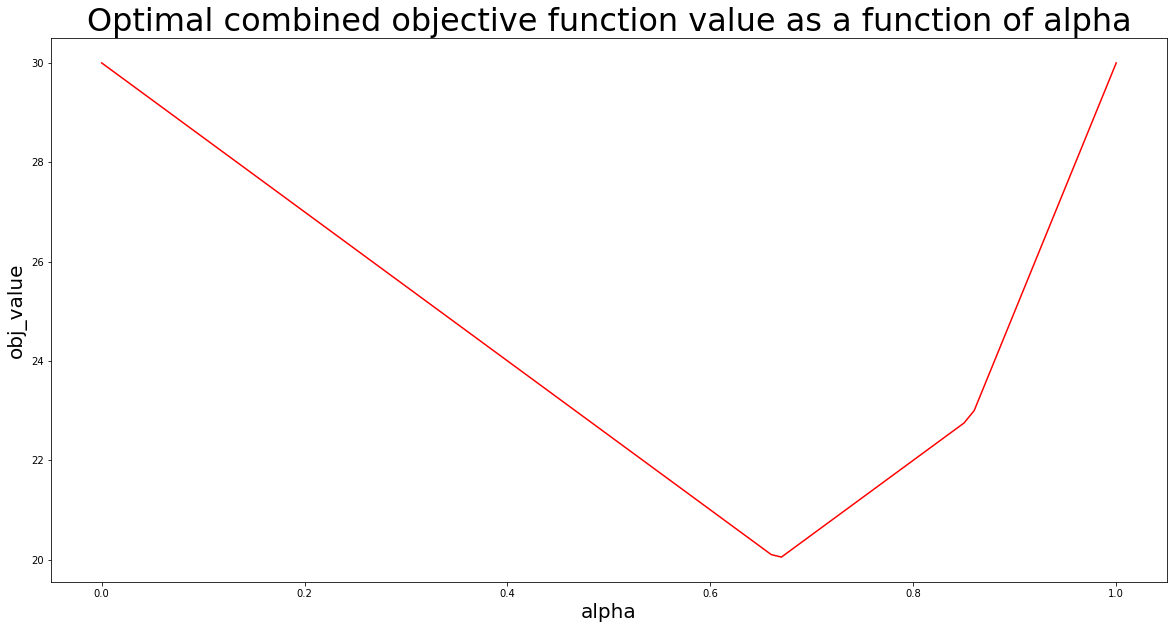
For at konstruere en sådan tilgang prøver jeg alfa i trin på 0,01. For hver værdi af alpha gentager jeg problemet ved hjælp af PuLP – og løser det.
Jeg gemmer mine resultater på en liste og visualiserer resultatet ved hjælp af matplotlib.pyplot:
# importer matplotlib.pyplot import matplotlib.pyplot as plt # importer pandaer og følelsesløs for at kunne gemme data i DataFrame-format import numpy as np import pandas as pd # definer trinstørrelse stepSize = 0.01 # initialiser tom DataFrame til lagring af optimeringsresultater solutionTable = pd.DataFrame(columns=["alpha","x1_opt","x2_opt","obj_value"]) # gentag gennem alfaværdier fra 0 til 1 med stepSize, og skriv PuLP-løsninger i løsningstabel for i in range(0,101,int(stepSize*100)): # erklær problemet igen linearProblem = pulp.LpProblem("Multi-objective linear maximization",pulp.LpMaximize) # tilføj objektivfunktionen ved samplet alfa linearProblem += (i/100)*(2*x1+3*x2)+(1-i/100)*(4*x1-2*x2) # tilføj begrænsningerne linearProblem += x1 + x2 <= 10 linearProblem += 2*x1 + x2 <= 15 # løs problemet solution = linearProblem.solve() # skriv løsninger i DataFrame solutionTable.loc[int(i/(stepSize*100))] = [i/100, pulp.value(x1), pulp.value(x2), pulp.value(linearProblem.objective)] # visualiser optimeringsresultatet ved hjælp af matplotlib.pyplot # - indstil figurstørrelse plt.figure(figsize=(20,10)) # - opret linieplot plt.plot(solutionTable["alpha"],solutionTable["obj_value"],color="red") # - tilføj akseetiketter plt.xlabel("alpha",size=20) plt.ylabel("obj_value",size=20) # - tilføj plottitel plt.title("Optimal combined objective function value as a function of alpha",size=32) # - vis plot plt.show()

For at fuldføre denne artikel udskriver jeg hovedet på optimeringsresultatet DataFrame-tabellen:
solutionTable.head()
| alpha | x1_opt | x2_opt | obj_value | |
|---|---|---|---|---|
| 0 | 0.00 | 7.5 | 0.0 | 30.00 |
| 1 | 0.01 | 7.5 | 0.0 | 29.85 |
| 2 | 0.02 | 7.5 | 0.0 | 29.70 |
| 3 | 0.03 | 7.5 | 0.0 | 29.55 |
| 4 | 0.04 | 7.5 | 0.0 | 29.40 |

Industriingeniør som gerne beskæftiger sig med optimering, simulation og matematisk modellering i R, SQL, VBA og Python




Leave a Reply