Geografisk kundegruppering (i R)

Giver et kodningseksempel på, hvordan man udfører rumlig nærhedskundeklyngning, anvendelig f.eks. når man søger efter flere tyngdepunkter (dvs. når man ønsker at løse et problem med flere lagerlokaliteter). Logikken og tilgangen er den samme som i enhver form for afstandsbaseret klyngeproblem.

Jeg vil anvende k-betyder clustering til gruppering af kunder baseret på deres rumlige afstand.

Algoritmen for k-means clustering er velforklaret, f.eks. i denne artikel: https://www.datanovia.com/en/lessons/k-means-clustering-in-r-algorith-and-practical-examples/

Først definerer jeg en dataramme indeholdende tilfældige bredde- og længdegradskoordinater, der repræsenterer tilfældigt distribuerede kunder.

customer_df <- as.data.frame(matrix(nrow=1000,ncol=2))
colnames(customer_df) <- c("lat","long")
customer_df$lat <- runif(n=1000,min=-90,max=90)
customer_df$long <- runif(n=1000,min=-180,max=180)

Her ser du overskriften på datarammen:

head(customer_df)

##          lat       long
## 1  67.260409   47.08063
## 2  55.400065   55.46616
## 3 -47.152065 -107.63843
## 4 -84.266658 -163.62681
## 5  -6.012361  103.34046
## 6 -10.717590  -59.64681

Standard k-betyder klyngealgoritmen vælger k tilfældige startpunkter og definerer dem som klyngecentrene. Algoritmen tildeler derefter datapunkter til hvert klyngecenter baseret på minimal afstand.

I dette tilfælde ønsker vi senere at bruge klyngealgoritmen til at løse facilitetsplaceringsproblemer, idet vi overvejer, at flere lagre skal lokaliseres. Jeg synes derfor mere hensigtsmæssigt at vælge klyngecentre, der er rimeligt distanceret fra hinanden. Til dette definerer jeg en funktion, der vælger det definerede antal startcentre baseret på længdegradsdimensionen af det geografiske datasæt:

initial_centers <- function(customers,centers){
  quantiles <- c()
  for(i in 1:centers){
    quantiles <- c(quantiles,i*as.integer(nrow(customers)/centers))
  }
  quantiles
}

Vi kan nu anvende ovenstående funktion i kombination med kmeans-funktionen fra R-basispakken. I dette eksempel udleder jeg fire nærhedsbaserede kundegrupper.

cluster_obj <- kmeans(customer_df,centers=customer_df[initial_centers(customer_df,4),])
head(cluster_obj)

## $cluster
##    [1] 4 4 1 1 2 1 2 4 1 2 1 4 3 4 4 1 1 1 2 2 3 2 1 3 2 3 1 4 2 4 4 2 4 2
##   [35] 1 4 4 2 2 1 3 2 2 1 3 2 4 3 2 1 1 2 2 3 4 1 4 2 2 3 2 1 2 1 2 2 2 3
##   [69] 1 4 3 3 2 1 4 3 1 1 3 1 2 1 2 1 1 4 2 4 1 2 2 1 4 3 4 2 1 2 3 4 1 2
##  [103] 3 3 4 4 4 1 4 3 1 4 1 2 2 1 3 2 3 2 4 3 4 3 2 1 1 2 2 2 4 4 4 1 2 2
##  [137] 3 3 2 4 4 3 4 1 1 1 3 3 4 4 1 1 2 4 3 4 4 2 2 1 3 2 4 3 2 1 1 2 1 1
##  [171] 2 1 1 1 4 3 3 1 2 3 2 4 2 2 2 4 3 2 1 4 1 2 4 2 3 2 2 2 2 2 1 2 2 1
##  [205] 2 1 2 3 3 2 3 1 2 1 2 4 1 1 2 4 3 2 4 2 1 4 4 3 1 1 2 1 2 2 3 2 1 1
##  [239] 3 1 3 1 2 1 2 1 1 4 1 1 2 2 1 2 1 4 1 4 2 2 2 2 4 4 1 3 3 1 1 4 3 4
##  [273] 4 4 1 2 2 1 4 1 2 4 2 1 4 2 4 2 3 4 4 4 2 2 1 4 2 4 4 1 2 1 2 1 2 3
##  [307] 1 1 1 1 2 3 3 3 1 4 4 1 2 1 4 1 4 3 2 4 3 2 1 2 2 4 2 4 2 2 2 4 2 1
##  [341] 3 2 1 3 3 2 1 1 3 1 4 1 2 1 4 1 2 3 2 1 4 2 3 1 3 1 1 2 2 2 2 2 1 3
##  [375] 2 2 1 2 4 4 1 3 1 2 3 4 2 4 4 1 1 2 4 4 4 2 3 4 1 3 2 3 4 1 3 3 1 4
##  [409] 2 1 4 1 3 2 1 3 3 2 2 2 1 2 3 1 2 4 4 2 2 4 3 4 3 1 1 3 1 3 4 2 4 3
##  [443] 3 3 4 1 1 2 1 3 2 1 1 2 1 4 2 2 1 1 2 1 2 4 2 4 3 2 1 1 1 4 2 3 1 4
##  [477] 3 1 2 1 1 1 2 3 4 3 2 3 4 4 2 1 3 2 1 4 4 2 4 2 3 1 2 2 3 4 2 3 2 4
##  [511] 3 4 2 4 2 1 3 2 1 4 2 4 3 1 1 4 2 2 2 1 4 2 1 3 1 4 1 4 2 3 4 3 1 2
##  [545] 2 2 2 2 2 2 2 2 4 4 1 4 1 2 2 1 1 1 2 3 3 1 1 2 2 3 4 3 2 2 2 1 1 3
##  [579] 4 2 1 4 1 3 3 1 1 1 2 3 1 2 3 1 4 4 1 1 3 1 4 1 2 3 3 2 4 4 2 4 2 2
##  [613] 2 3 1 1 4 2 3 4 1 4 4 2 2 1 4 3 3 4 4 1 1 3 4 3 1 1 2 3 3 3 3 1 1 1
##  [647] 4 1 2 1 2 4 2 4 2 2 3 4 4 2 4 1 2 1 1 4 2 1 1 2 1 4 4 1 3 3 1 3 4 4
##  [681] 2 2 4 3 1 2 3 2 4 3 2 4 3 4 1 4 4 1 3 1 3 3 4 2 1 4 4 2 2 2 2 3 1 1
##  [715] 1 2 1 4 1 3 1 2 2 4 3 3 2 2 1 3 2 2 1 1 3 4 3 3 1 1 2 1 1 4 2 4 1 4
##  [749] 2 2 2 2 3 1 2 1 1 1 2 1 3 2 1 3 2 3 2 2 1 2 4 3 4 1 4 2 3 1 3 1 3 2
##  [783] 3 1 1 1 1 1 4 2 2 1 2 1 4 1 4 3 4 1 2 1 1 4 2 1 4 4 3 4 2 3 1 3 2 3
##  [817] 1 3 4 2 4 1 3 2 1 3 3 1 1 1 1 4 2 2 4 1 1 3 4 1 2 3 2 4 1 1 1 3 2 2
##  [851] 1 3 3 2 3 1 2 2 3 2 1 4 1 1 1 3 2 1 3 1 2 3 2 4 2 2 2 2 1 3 4 3 1 4
##  [885] 2 3 2 2 3 4 4 2 2 1 3 4 4 1 4 4 3 1 2 4 2 1 1 1 2 4 3 1 1 3 1 3 1 1
##  [919] 4 3 1 2 1 3 2 4 2 1 4 2 1 3 1 2 1 3 3 1 2 1 1 1 1 1 1 3 4 4 2 1 2 2
##  [953] 2 1 1 1 4 2 3 4 3 4 1 2 3 3 1 4 2 1 1 3 1 3 4 1 3 1 3 1 3 3 1 4 3 4
##  [987] 1 3 2 4 4 2 3 4 3 2 4 2 3 2
## 
## $centers
##           lat        long
## 1   0.6938018 -122.442238
## 2  -5.3567099  123.957813
## 3 -46.9979863   -2.714282
## 4  48.9979562   15.062099
## 
## $totss
## [1] 13050174
## 
## $withinss
## [1] 1108924.4 1028012.3  423675.5  523506.7
## 
## $tot.withinss
## [1] 3084119
## 
## $betweenss
## [1] 9966055

Ovenfor ser du overskriften på resultatobjektet, der returneres af kmeans-funktionen. Nedenfor kombinerer jeg klyngeindekserne indeholdt af kmeans-objektet med kundedatarammen, således at vi nu har 3 kolonner. Dette vil give os mulighed for at lave ggplots osv.

result_df <- customer_df
result_df$group <- cluster_obj$cluster
head(result_df)

##          lat       long group
## 1  67.260409   47.08063     4
## 2  55.400065   55.46616     4
## 3 -47.152065 -107.63843     1
## 4 -84.266658 -163.62681     1
## 5  -6.012361  103.34046     2
## 6 -10.717590  -59.64681     1

Jeg fuldender dette indlæg ved at visualisere resultaterne i et ggplot (scatterplot ved hjælp af ggplot2 R-pakken). Til farvning brugte jeg viridis-pakken i R:

library(ggplot2)
library(viridis)

ggplot(result_df) + geom_point(mapping = aes(x=lat,y=long,color=group)) +
  xlim(-90,90) + ylim(-180,180) + scale_color_viridis(discrete = FALSE, option = "D") + scale_fill_viridis(discrete = FALSE)

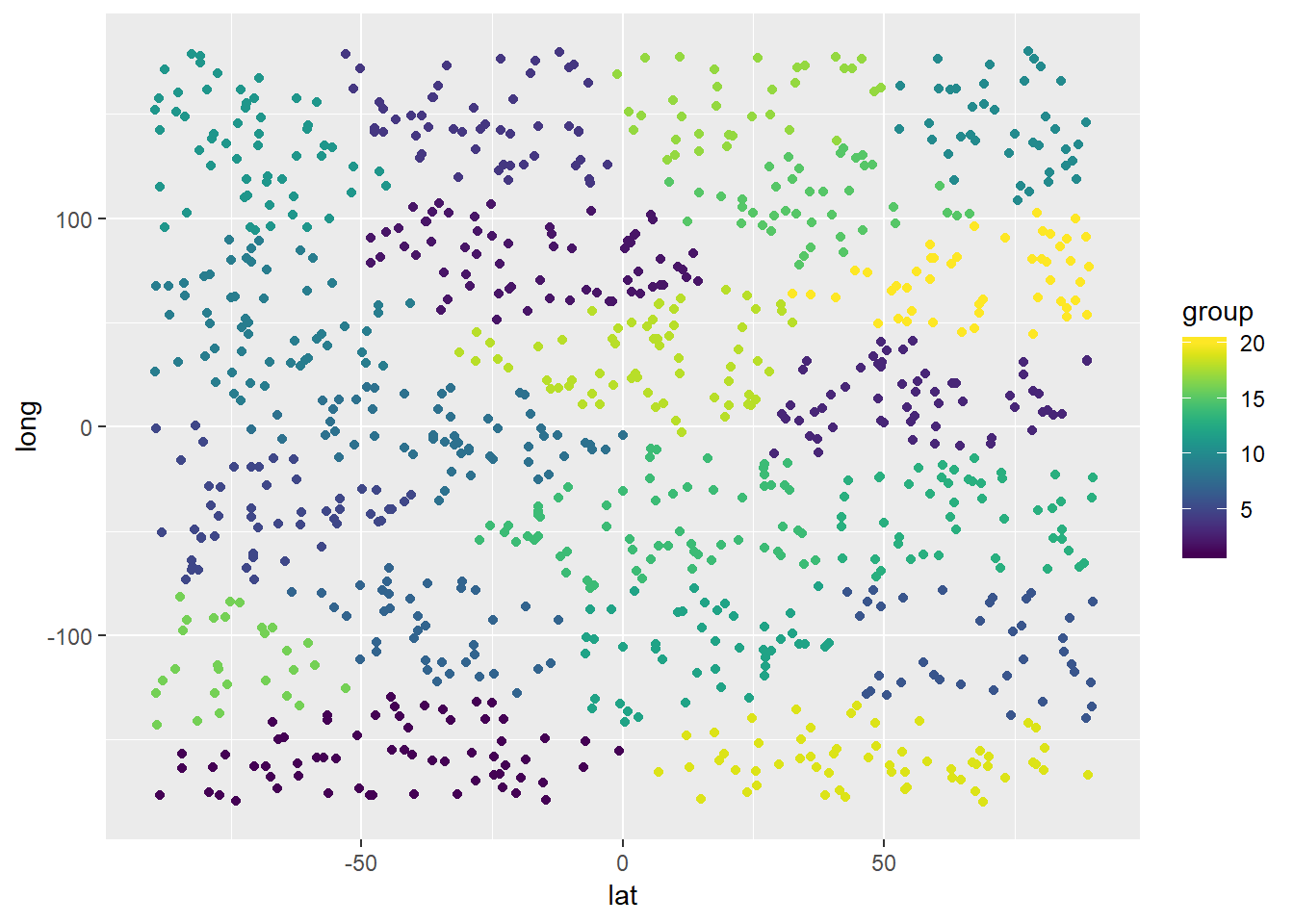
Lad os køre endnu en test med 20 varehuse:

cluster_obj <- kmeans(customer_df,centers=customer_df[initial_centers(customer_df,20),])
result_df$group <- cluster_obj$cluster
ggplot(result_df) + geom_point(mapping = aes(x=lat,y=long,color=group)) +
  xlim(-90,90) + ylim(-180,180) + scale_color_viridis(discrete = FALSE, option = "D") + scale_fill_viridis(discrete = FALSE)