Ausgangsprognose mit gleitendem Mittelwert

In einem früheren Beitrag habe ich CAGR-basierte Prognosen erklärt. Die CAGR-basierte Prognose ist eine sehr einfache Prognosemethode, die häufig in der Industrie eingesetzt wird, zB zur Prognose von Absatz und Produktionsleistung.

Einfache Prognosemodelle haben Vorteile. Sie sind leicht verständlich und einfach umzusetzen. Zudem enthalten sie wenige Parameter und sind damit in ihren Kernannahmen sehr präzise. Insofern kann man sagen, dass einfache Prognoseverfahren in vielen Fällen die besten Prognoseverfahren sind. Mit anderen Worten: Wenn Sie versuchen, die Zukunft vorherzusagen, sollten Sie dies am besten mit einem Prognosemodell tun, das Sie vollständig verstehen und das Sie jederzeit jedem erklären können.

In diesem Beitrag möchte ich Zeitreihenprognosen basierend auf einer einfachen Berechnung des gleitenden Durchschnitts vorstellen. Gleitende Durchschnitte, auch rollierende Durchschnitte oder rollierende Mittelwerte genannt, werden zur Analyse und Vorverarbeitung historischer Zeitreihendaten verwendet. Dennoch können sie zum Erstellen eines einfachen Prognosealgorithmus verwendet werden.

Ich unterscheide einfache gleitende Durchschnittsprognosen in zwei Kategorien:

(a) Prognosen aus historischen Daten durch Berechnung eines gleitenden Durchschnitts

(b) wie (a), jedoch mit einem zusätzlichen intrinsischen Wachstumsparameter

Kategorie (b) ist somit eine Kombination aus CAGR-basierter Prognose und gleitender Durchschnittsprognose.

Wie CAGR-basierte Prognosen können einfache gleitende Durchschnittsprognosen nur für begrenzte Zeithorizonte verwendet werden.

Ich implementiere einen solchen Prognoseansatz im folgenden Codierungsbeispiel mit einer Funktion, die einen gleitenden Durchschnitt definierter Länge berechnet. Ich implementiere diese Funktion in R und wende sie für die Vorhersage zukünftiger Werte an. Ich nenne die Funktion „sma_forecast“. Es ist im folgenden R-Code implementiert:

sma_forecast = function(past,length){
  
  future = rep(0,times = length)
  
  prediction = c(past,future)
  
  for(i in (length(past)+1):length(prediction)){
    prediction[i] = mean(prediction[(i-length(past)):(i-1)])
  }
  
  return(prediction)
}

Der nächste Schritt in diesem Workflow ist das Einlesen historischer Daten. In diesem Fall lese ich Daten zur jährlichen Produktionsleistung der Automobilindustrie nach Ländern ein, gemessen in der Anzahl der in einem bestimmten Jahr in einem bestimmten Land produzierten Einheiten. Der letzte Schritt ist die Berechnung der Prognose mithilfe von sma_forecast. All dies geschieht im folgenden Codierungsbeispiel mit R:

library(readxl)

data_df = as.data.frame(read_xls("oica.xls"))

head(data_df)

##   year   country    total
## 1 2018 Argentina   466649
## 2 2018   Austria   164900
## 3 2018   Belgium   308493
## 4 2018    Brazil  2879809
## 5 2018    Canada  2020840
## 6 2018     China 27809196

tail(data_df)

##     year    country    total
## 835 1999     Turkey   297862
## 836 1999    Ukraine     1918
## 837 1999         UK  1973519
## 838 1999        USA 13024978
## 839 1999 Uzbekistan    44433
## 840 1999     Others    11965

library(dplyr)
data_df = filter(data_df,country=="USA")

library(ggplot2)
ggplot(data_df) + 
  geom_path(mapping = aes(x = year, y = total/1000000), 
            size = 2, 
color = "red") + 
  labs(title = "US automotive industry production output",
       subtitle = "historical OICA data, for 1999 - 2018") +
  xlab("year") +
  ylab("output [millions of units]") + 
  ylim(0,15)

library(dplyr)
data_df = data_df %>% arrange(desc(-year))

predictionVals = sma_forecast(past=data_df$total,length = 10)

plot_df = as.data.frame(matrix(nrow=length(predictionVals),ncol= 4))
colnames(plot_df) = c("year","country","total","category")
plot_df$total = predictionVals
plot_df$category[1:nrow(data_df)] = "history"
plot_df$category[(nrow(data_df)+1):length(predictionVals)] = "prediction"
plot_df$year = data_df$year[1]:(data_df$year[1]+length(predictionVals)-1)
plot_df$country = data_df$country[1]

ggplot(plot_df) +
  geom_point(mapping = aes(x = year,
                          y = total/1000000,
                          color = category),
             size = 2) +
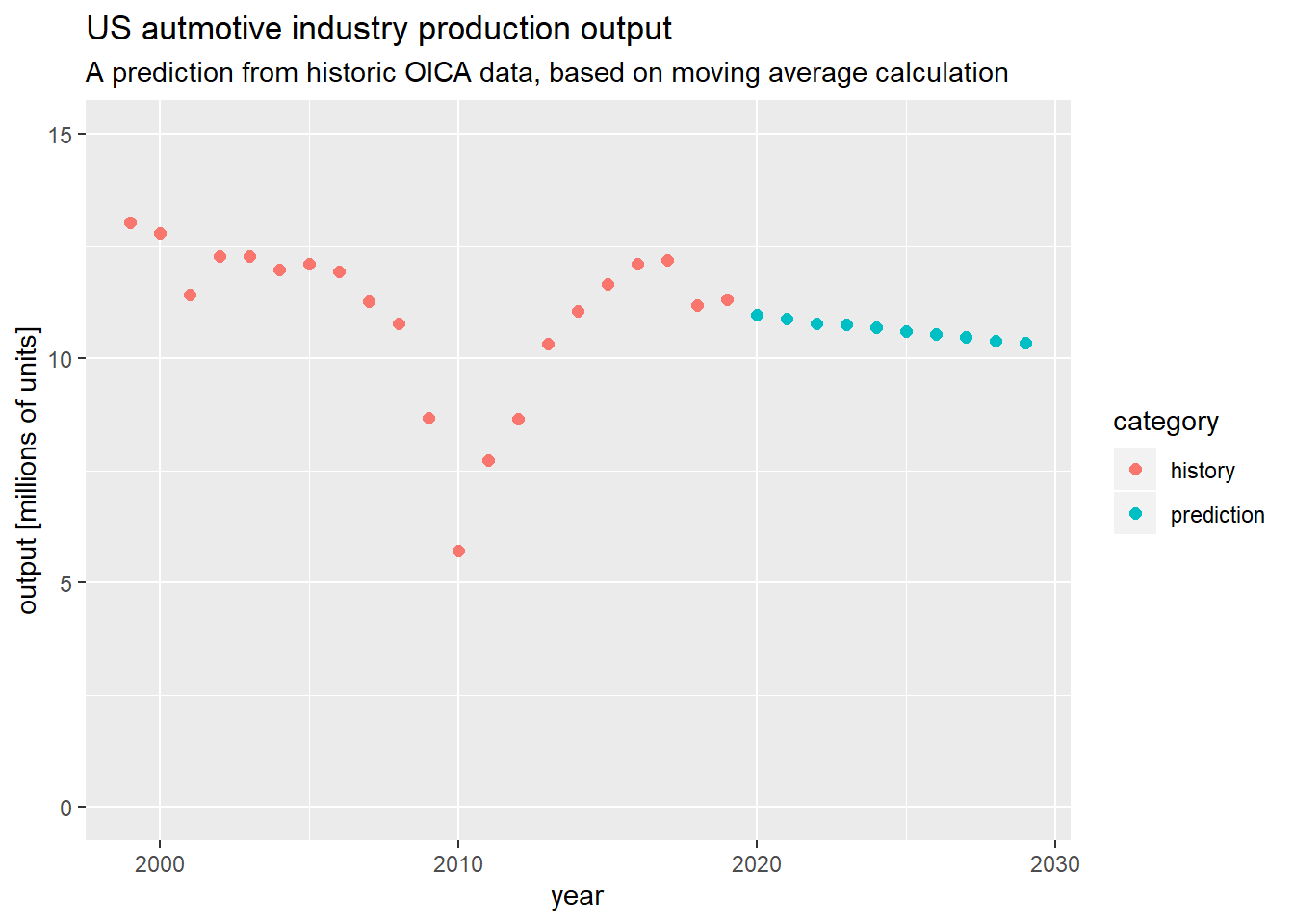
  labs(title = "US autmotive industry production output",
       subtitle = "A prediction from historic OICA data, based on moving average calculation") +
  xlab("year") +
  ylab("output [millions of units]") +
  ylim(0,15)

Ich beende mein Beispiel an dieser Stelle.

Dinge, die ich hätte hinzufügen können:

(a) Aufteilung in Trainings- und Testset zur Bewertung der Methode

(b) Bewerten Sie die Methode für verschiedene Länder, Zeitintervalle und Vorhersagelängen

(d) …

Wenn Sie diesen Beitrag interessant fanden, können Sie sich meine anderen Beiträge ansehen, z. B. zu CAGR-basierten Prognosen, dem Erhalten und Analysieren von OICA-Daten, Zeitreihenanalyse, linearer Programmierung, öffentlichen Quellen für Verkaufsdaten der Automobilindustrie usw.