In diesem Beispiel betrachte ich die Identifizierung von Kundenclustern basierend auf der euklidischen Distanz. Dies ist bspw. bei der Suche nach mehreren optimalen Standorten hilfreich. Ziel ist es dabei, eine Heuristik zu erarbeiten, mit der sich die Kunden gruppieren lassen, um im Nachgang ein Lager im Schwerpunkt der jeweiligen Gruppe platzieren zu können. Diese Heuristik kann konventionellen Lösungsverfahren gegenübergestellt werden und stellt einen einfachen und effizienten Ansatz dar, welcher sich in der Praxis von den meisten SCM Analysten schnell und ohne Beratungsbedarf oder Trainingsaufwand umsetzen lässt.
Distanz-basierte Kundengruppierung mittels k-means Clustering
Ich werde k-means Clustering zur Gruppierung von Kunden anwenden. Als Metrik dient mir die euklidische Distanz.
Der Algorithmus für das k-means Clusteringverfahren ist gut erklärt, z.B. in diesem Artikel: https://www.datanovia.com/de/lessons/k-means-clustering-in-r-algorith-and-practical-examples/
Zuerst definiere ich einen Datenrahmen mit zufälligen Längen- und Breitengradkoordinaten. Diese Daten simulieren eine fiktive Kundenpopulation und deren räumliche Verteilung.
customer_df <- as.data.frame(matrix(nrow=1000,ncol=2))
colnames(customer_df) <- c("lat","long")
customer_df$lat <- runif(n=1000,min=-90,max=90)
customer_df$long <- runif(n=1000,min=-180,max=180)Nachstehend zeige ich den Kopf des Datenrahmens an:
head(customer_df)## lat long
## 1 67.260409 47.08063
## 2 55.400065 55.46616
## 3 -47.152065 -107.63843
## 4 -84.266658 -163.62681
## 5 -6.012361 103.34046
## 6 -10.717590 -59.64681Der gewöhnliche k-means Clusteringalgorithmus wählt k zufällige Startpunkte aus und definiert diese als Cluster-Zentren. Der Algorithmus weist dann jedem Clusterzentrum Datenpunkte zu, basierend auf kürzester Distanz bzw. nächster Nähe.
Wahl der Startpunkte für das k-means Clustering
In diesem Fall möchten wir später den Clustering-Algorithmus zur Lösung von Standortproblemen verwenden, wobei mehrere zu lokalisierende Lagerstandorte berücksichtigt werden müssen. Ich halte es daher für angemessener, Cluster-Zentren auszuwählen, die ausreichend weit voneinander entfernt sind. Dazu definiere ich eine Funktion. Diese wählt eine definierte Anzahl von Startzentren basierend auf Längengraddimensionen des Geodatensatzes aus:
initial_centers <- function(customers,centers){
quantiles <- c()
for(i in 1:centers){
quantiles <- c(quantiles,i*as.integer(nrow(customers)/centers))
}
quantiles
}Anwendung der kmeans()-Funktion in R
Wir können nun die obige Funktion in Kombination mit der kmeans-Funktion aus dem R-Basispaket anwenden. In diesem Beispiel leite ich vier Proximity-basierte Kundengruppen ab.
cluster_obj <- kmeans(customer_df,centers=customer_df[initial_centers(customer_df,4),])
head(cluster_obj)## $cluster
## [1] 4 4 1 1 2 1 2 4 1 2 1 4 3 4 4 1 1 1 2 2 3 2 1 3 2 3 1 4 2 4 4 2 4 2
## [35] 1 4 4 2 2 1 3 2 2 1 3 2 4 3 2 1 1 2 2 3 4 1 4 2 2 3 2 1 2 1 2 2 2 3
## [69] 1 4 3 3 2 1 4 3 1 1 3 1 2 1 2 1 1 4 2 4 1 2 2 1 4 3 4 2 1 2 3 4 1 2
## [103] 3 3 4 4 4 1 4 3 1 4 1 2 2 1 3 2 3 2 4 3 4 3 2 1 1 2 2 2 4 4 4 1 2 2
## [137] 3 3 2 4 4 3 4 1 1 1 3 3 4 4 1 1 2 4 3 4 4 2 2 1 3 2 4 3 2 1 1 2 1 1
## [171] 2 1 1 1 4 3 3 1 2 3 2 4 2 2 2 4 3 2 1 4 1 2 4 2 3 2 2 2 2 2 1 2 2 1
## [205] 2 1 2 3 3 2 3 1 2 1 2 4 1 1 2 4 3 2 4 2 1 4 4 3 1 1 2 1 2 2 3 2 1 1
## [239] 3 1 3 1 2 1 2 1 1 4 1 1 2 2 1 2 1 4 1 4 2 2 2 2 4 4 1 3 3 1 1 4 3 4
## [273] 4 4 1 2 2 1 4 1 2 4 2 1 4 2 4 2 3 4 4 4 2 2 1 4 2 4 4 1 2 1 2 1 2 3
## [307] 1 1 1 1 2 3 3 3 1 4 4 1 2 1 4 1 4 3 2 4 3 2 1 2 2 4 2 4 2 2 2 4 2 1
## [341] 3 2 1 3 3 2 1 1 3 1 4 1 2 1 4 1 2 3 2 1 4 2 3 1 3 1 1 2 2 2 2 2 1 3
## [375] 2 2 1 2 4 4 1 3 1 2 3 4 2 4 4 1 1 2 4 4 4 2 3 4 1 3 2 3 4 1 3 3 1 4
## [409] 2 1 4 1 3 2 1 3 3 2 2 2 1 2 3 1 2 4 4 2 2 4 3 4 3 1 1 3 1 3 4 2 4 3
## [443] 3 3 4 1 1 2 1 3 2 1 1 2 1 4 2 2 1 1 2 1 2 4 2 4 3 2 1 1 1 4 2 3 1 4
## [477] 3 1 2 1 1 1 2 3 4 3 2 3 4 4 2 1 3 2 1 4 4 2 4 2 3 1 2 2 3 4 2 3 2 4
## [511] 3 4 2 4 2 1 3 2 1 4 2 4 3 1 1 4 2 2 2 1 4 2 1 3 1 4 1 4 2 3 4 3 1 2
## [545] 2 2 2 2 2 2 2 2 4 4 1 4 1 2 2 1 1 1 2 3 3 1 1 2 2 3 4 3 2 2 2 1 1 3
## [579] 4 2 1 4 1 3 3 1 1 1 2 3 1 2 3 1 4 4 1 1 3 1 4 1 2 3 3 2 4 4 2 4 2 2
## [613] 2 3 1 1 4 2 3 4 1 4 4 2 2 1 4 3 3 4 4 1 1 3 4 3 1 1 2 3 3 3 3 1 1 1
## [647] 4 1 2 1 2 4 2 4 2 2 3 4 4 2 4 1 2 1 1 4 2 1 1 2 1 4 4 1 3 3 1 3 4 4
## [681] 2 2 4 3 1 2 3 2 4 3 2 4 3 4 1 4 4 1 3 1 3 3 4 2 1 4 4 2 2 2 2 3 1 1
## [715] 1 2 1 4 1 3 1 2 2 4 3 3 2 2 1 3 2 2 1 1 3 4 3 3 1 1 2 1 1 4 2 4 1 4
## [749] 2 2 2 2 3 1 2 1 1 1 2 1 3 2 1 3 2 3 2 2 1 2 4 3 4 1 4 2 3 1 3 1 3 2
## [783] 3 1 1 1 1 1 4 2 2 1 2 1 4 1 4 3 4 1 2 1 1 4 2 1 4 4 3 4 2 3 1 3 2 3
## [817] 1 3 4 2 4 1 3 2 1 3 3 1 1 1 1 4 2 2 4 1 1 3 4 1 2 3 2 4 1 1 1 3 2 2
## [851] 1 3 3 2 3 1 2 2 3 2 1 4 1 1 1 3 2 1 3 1 2 3 2 4 2 2 2 2 1 3 4 3 1 4
## [885] 2 3 2 2 3 4 4 2 2 1 3 4 4 1 4 4 3 1 2 4 2 1 1 1 2 4 3 1 1 3 1 3 1 1
## [919] 4 3 1 2 1 3 2 4 2 1 4 2 1 3 1 2 1 3 3 1 2 1 1 1 1 1 1 3 4 4 2 1 2 2
## [953] 2 1 1 1 4 2 3 4 3 4 1 2 3 3 1 4 2 1 1 3 1 3 4 1 3 1 3 1 3 3 1 4 3 4
## [987] 1 3 2 4 4 2 3 4 3 2 4 2 3 2
##
## $centers
## lat long
## 1 0.6938018 -122.442238
## 2 -5.3567099 123.957813
## 3 -46.9979863 -2.714282
## 4 48.9979562 15.062099
##
## $totss
## [1] 13050174
##
## $withinss
## [1] 1108924.4 1028012.3 423675.5 523506.7
##
## $tot.withinss
## [1] 3084119
##
## $betweenss
## [1] 9966055Oben wurde der Kopf des Ergenisdatenrahmens angezeigt. Dieser wurde von der kmeans-Funktion zurückgegeben. Nachstehend kombiniere ich die im k-means Objekt enthaltenen Cluster-Indizes mit dem Kundendatenrahmen, sodass ich jetzt 3 Spalten habe. Dies ermöglicht es mir bspw. Plots mit ggplot2 zu erstellen.
result_df <- customer_df
result_df$group <- cluster_obj$cluster
head(result_df)## lat long group
## 1 67.260409 47.08063 4
## 2 55.400065 55.46616 4
## 3 -47.152065 -107.63843 1
## 4 -84.266658 -163.62681 1
## 5 -6.012361 103.34046 2
## 6 -10.717590 -59.64681 1Visualisierung der Gruppierungsergebnisse mittels ggplot2 in R
Ich vervollständige diesen Beitrag, indem ich die Ergebnisse in einem ggplot visualisiere (Streudiagramm mit dem ggplot2 R-Paket). Zum Färben habe ich das Viridis-Paket in R verwendet:
library(ggplot2)
library(viridis)ggplot(result_df) + geom_point(mapping = aes(x=lat,y=long,color=group)) +
xlim(-90,90) + ylim(-180,180) + scale_color_viridis(discrete = FALSE, option = "D") + scale_fill_viridis(discrete = FALSE) 
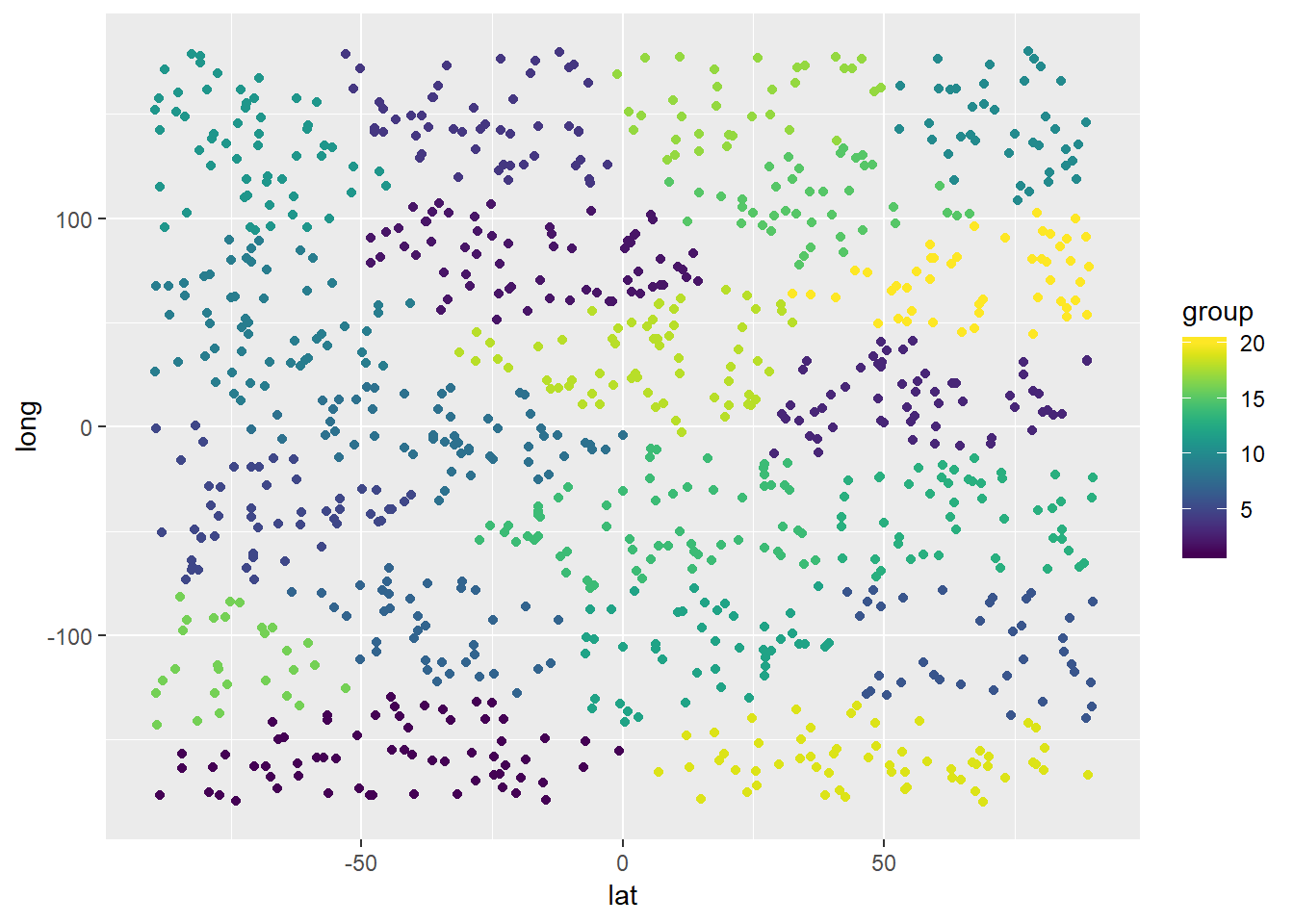
Ich führe nun einen weiteren Test mit 20 potenziellen Lagerstandorten und somit 20 Kundengruppen durch. Die Implementierung und die visualisierten Ergebnisse sind nachstehend aufgeführt:
cluster_obj <- kmeans(customer_df,centers=customer_df[initial_centers(customer_df,20),])
result_df$group <- cluster_obj$cluster
ggplot(result_df) + geom_point(mapping = aes(x=lat,y=long,color=group)) +
xlim(-90,90) + ylim(-180,180) + scale_color_viridis(discrete = FALSE, option = "D") + scale_fill_viridis(discrete = FALSE) 
Relevante Weiterentwicklungen des Gruppierungsansatzes
Wie anfangs in diesem Artikel dargestellt eignet sich dieses Gruppierungsverfahren vor allen in Kombination mit einer darauf folgenden Schwerpunktermittlung. Die Schwerpunktermittlung identifiziert für jedes Kundencluster des Massenschwerpunkt. Daraus ergibt sich eine Heuristik für die optimale Lagerplatzzuordnung je Kundengruppe. In Kombination, d.h. Kundengruppierung + Schwerpunktermittlung, ergibt sich ein Verfahren zur optimalen Lagerplatzauswahl im Falle von n Lagerstandorten.
Ich habe auf diesem Blog bereits weitere Artikel zur Schwerpunktermittlung publiziert. In diesen kann sowohl das Verfahren zur Schwerpunktermittlung sowie die Kombination aus Clustering und Schwerpunktermittlung im Detail nachvollzogen werden.

Wirtschaftsingenieur mit Interesse an Optimierung, Simulation und mathematischer Modellierung in R, SQL, VBA und Python




Leave a Reply