Platzierung mehrerer Lager im Massenmittelpunkt (mit R)

In einem früheren Beitrag habe ich bereits gezeigt wie das Problem der Bestimmung eines einzelnen Lagerstandorts ganz einfach gelöst werden kann. Ich hatte dabei den Massenschwerpunkt der relevanten räumlich verteilten Metrik indentifiziert. In diesem Beitrag möchte ich nicht nur ein sondern mehrere Lagerstandorte bestimmen und festlegen.

In http://www.supplychaindataanalytics.com/single-warehouse-problem-locating-warehouse-at-center-of-mass-using-r/ habe ich eine Funktion zum Lokalisieren eines einzelnen Lagers in seinem Massenschwerpunkt bereitgestellt.

In http://www.supplychaindataanalytics.com/proximity-based-spatial-customer-grouping-in-r habe ich gezeigt, wie Kunden basierend auf räumlichem Proximity-Clustering gruppiert werden können.

# siehe Beispiel hier: http://www.supplychaindataanalytics.com/single-warehouse-problem-locating-warehouse-at-center-of-mass-using-r/
center_of_mass <- function(x,y,w){
  c(crossprod(x,w)/sum(w),crossprod(y,w)/sum(w))
}

# siehe Beispiel hier: http://www.supplychaindataanalytics.com/proximity-based-spatial-customer-grouping-in-r
initial_centers <- function(customers,centers){
  quantiles <- c()
  for(i in 1:centers){
    quantiles <- c(quantiles,i*as.integer(nrow(customers)/centers))
  }
  quantiles
}

Wir werden diese beiden Ansätze kombinieren um ein Problem mit mehreren Lagerstandorten mit Hilfe der Schwerpunkttheorie zu lösen. Dieser Ansatz ist anwendbar wenn wir bereits wissen, wie viele Lagerstandorte wir betreiben möchten. Der Ansatz aus dem vorliegenden Beitrag eignet sich nicht dafür ein Problem zu lösen bei dem wir noch nicht wissen wie viele Lagerhallen benötigt werden.

Ich beginne mit der Erstellung eines Datenrahmens mit 1000 zufällig verteilten Kunden mit zufällig verteilter Nachfrage.

customer_df <- as.data.frame(matrix(nrow=1000,ncol=3))
colnames(customer_df) <- c("lat","long","demand")
customer_df$lat <- runif(n=1000,min=-90,max=90)
customer_df$long <- runif(n=1000,min=-180,max=180)
customer_df$demand <- runif(n=1000,min=0,max=10)
head(customer_df)

##         lat       long   demand
## 1 -42.50378  137.62188 9.608067
## 2  47.79308  101.30536 9.510299
## 3 -14.17326   24.38595 1.610305
## 4 -85.34352 -151.29061 6.394425
## 5 -26.31244  112.75030 6.972434
## 6  55.01428   58.17198 2.797564

Als nächstes gruppiere ich die Kunden nach dem in einem vorherigen Beitrag gezeigten Ansatz der räumlichen Nähe und wende die definierte Funktion initial_centers an. Ich möchte 20 Lagerhallen erstellen und so also auch einplanen. Ich erstellen also 20 Gruppen (= Cluster).

centeroids <- initial_centers(customer_df[,-3],20)
cluster_obj <- kmeans(customer_df[,-3],centers = customer_df[centeroids,-3])
customer_df$group <- cluster_obj$cluster
head(customer_df)

##         lat       long   demand group
## 1 -42.50378  137.62188 9.608067     2
## 2  47.79308  101.30536 9.510299     4
## 3 -14.17326   24.38595 1.610305     6
## 4 -85.34352 -151.29061 6.394425     8
## 5 -26.31244  112.75030 6.972434    18
## 6  55.01428   58.17198 2.797564    16

Wie oben gezeigt habe ich den Cluster-basierten Gruppenindex dem Kundendatenrahmen hinzugefügt.

Jetzt werde ich eine Funktion definieren, die jede Kundengruppe durchläuft und den Schwerpunkt identifiziert. Voraussetzung ist, dass ein Datenrahmen eingegeben wird, der eine Breiten-, Längen-, Bedarfs- und Gruppenspalte enthält – in genau diesem Format:

multiple_centers_of_mass <- function(df){
  result_df <- as.data.frame(matrix(nrow=nrow(df),ncol=6))
  colnames(result_df) <- c("lat","long","demand","group","com_lat","com_long")
  result_df[,c(1,2,3,4)] <- df
  for(i in 1:length(unique(df[,4]))){
    sub_df <- result_df[result_df$group==i,]
    com <- center_of_mass(sub_df$lat,sub_df$long,sub_df$demand)
    result_df$com_lat[result_df$group==i] <- com[1]
    result_df$com_long[result_df$group==i] <- com[2]
  }
  result_df
}

Testen wir die soeben definierte Funktion multiple_centers_of_mass:

com_df <- multiple_centers_of_mass(customer_df)
head(com_df)

##         lat       long   demand group   com_lat   com_long
## 1 -42.50378  137.62188 9.608067     2 -25.97973  158.17382
## 2  47.79308  101.30536 9.510299     4  63.58158   84.91329
## 3 -14.17326   24.38595 1.610305     6 -21.20417   26.80993
## 4 -85.34352 -151.29061 6.394425     8 -64.12072 -145.48419
## 5 -26.31244  112.75030 6.972434    18 -33.15564   99.15738
## 6  55.01428   58.17198 2.797564    16  35.04988   44.42388

Nun visualisieren wir die Testergebnisse mithilfe eines Streudiagramms aus dem Paket ggplot2 in R. Unten sind die Lagerorte (Massenschwerpunkte) angezeigt:

library(ggplot2)

lat_wh_vc <- unique(com_df$com_lat)
long_wh_vc <- unique(com_df$com_long)
warehouse_df <- as.data.frame(matrix(nrow=length(lat_wh_vc),ncol=2))
warehouse_df[,1] <- lat_wh_vc
warehouse_df[,2] <- long_wh_vc
colnames(warehouse_df) <- c("lat","long")
ggplot(warehouse_df) + geom_point(mapping = aes(x=lat,y=long)) + xlim(-90,90) + ylim(-180,180)

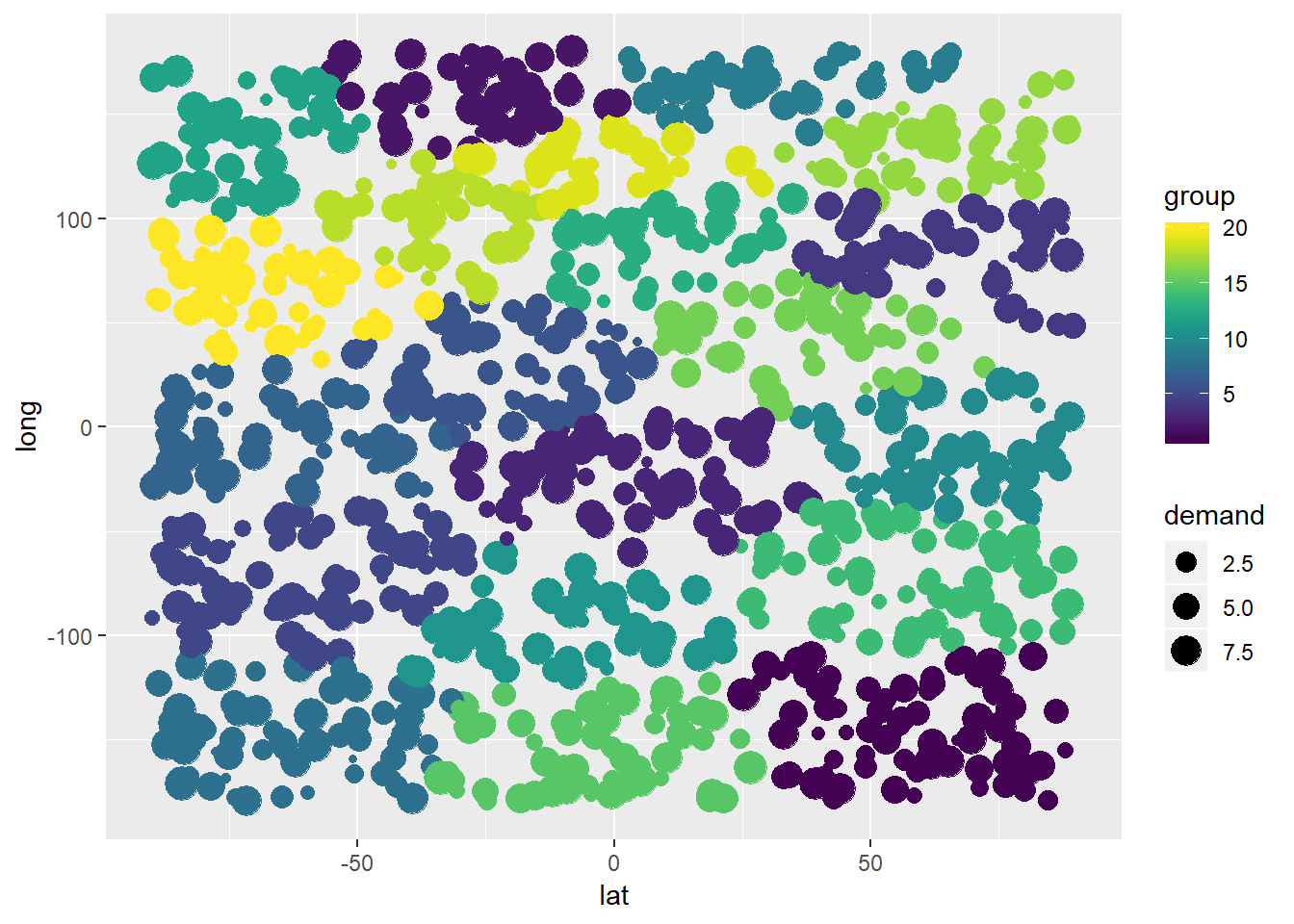
Die Kunden wurden wie folgt gruppiert:

library(viridis)

## Warning: package 'viridis' was built under R version 3.5.3

## Loading required package: viridisLite

ggplot(com_df) + geom_point(mapping = aes(x=lat,y=long,color=group,size=demand)) +
  xlim(-90,90) + ylim(-180,180) + scale_color_viridis(discrete = FALSE, option = "D") + scale_fill_viridis(discrete = FALSE)