Lineare Optimierung mit lpSolve in R

In diesem Beitrag möchte ich zeigen, wie ein einfaches lineares Optimierungsproblem mit lpSolve in R gelöst werden kann.

lpSolve ist ein R-Paket mit einer C-basierten Schnittstelle zu linearen Lösungsmaschinen.

In diesem Beispiel ist die Zielfunktion: f(x,y) = 2x + 3y, s.d. x >= 0, y >= 0 und x + y <= 3. Es gilt die Zielfunktion zu maximieren.

Nachstehend modelliere ich das Problem in R:

library(lpSolve)
f.obj <- c(2,3)                           # koeffizienten der zielfunktion
f.con <- matrix(c(1,1),nrow=1,byrow=TRUE) # koeffizienten der linearen NB
f.dir <- c("<=")                          # richtungen der NB
f.rhs <- c(3)                             # werte der NB

Nach erfolgter Modellierung lasse ich nun die Lösung ermitteln:

solution <- lp("max",f.obj,f.con,f.dir,f.rhs)
solution

## Success: the objective function is 9

Die optimale Lösung zu dem Problem (mit Optimalwert 9) ist die folgende:

solution$solution

## [1] 0 3

D.h. x = 0, y = 3.

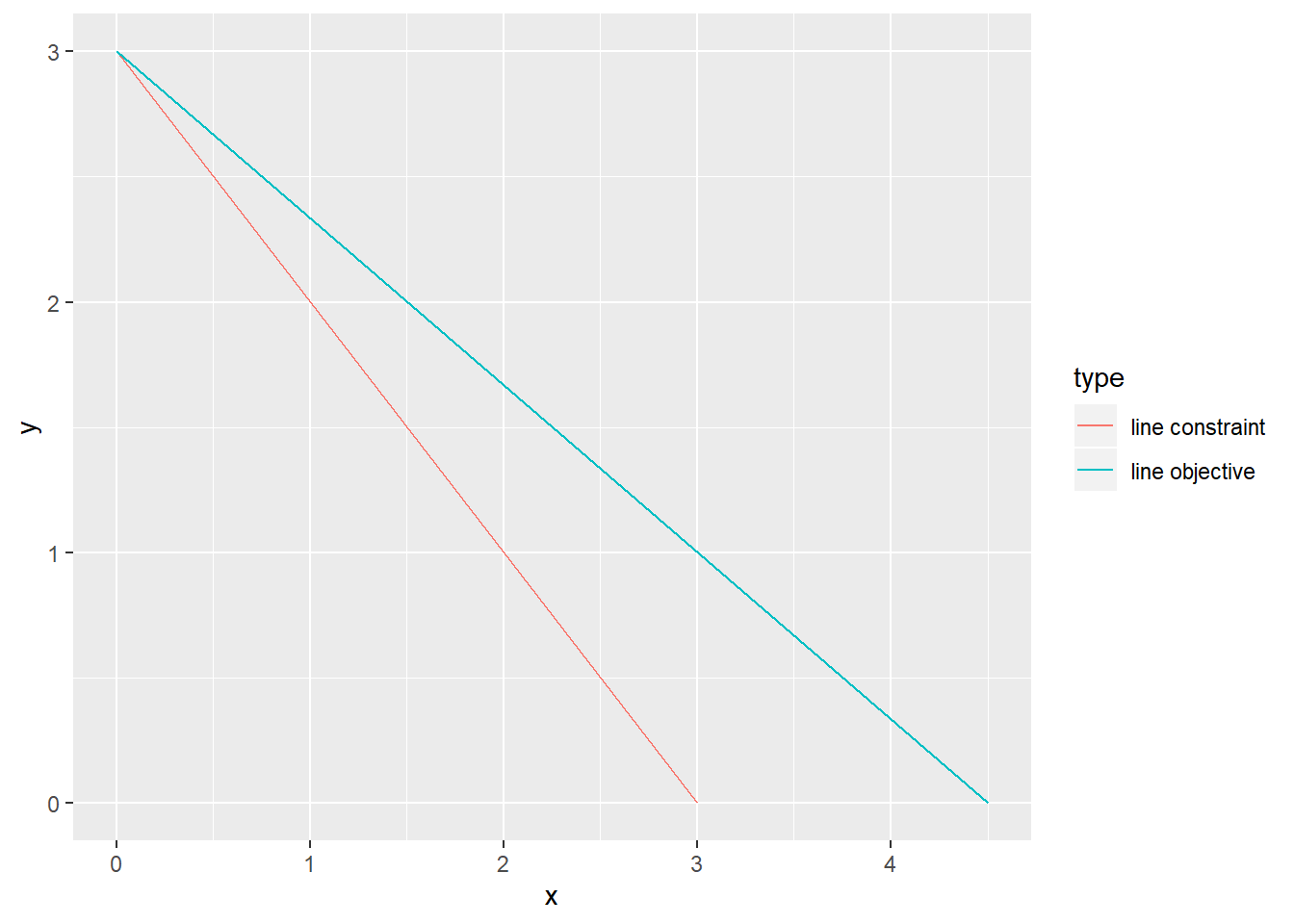
Wir können obiges Ergebnis mittels Graphiken validieren. Nachstehend plotte ich die Nebenbedingung (x+y<=3) und die Zielfunktion für den Zielfunktionswert 9.

library(ggplot2)
plot_df <- as.data.frame(matrix(nrow=4,ncol=3))
colnames(plot_df) <- c("x","y","type")
plot_df$x <- c(0,3,0,9/2)
plot_df$y <- c(3,0,9/3,0)
plot_df$type <- c("line constraint","line constraint", "line objective", "line objective")
ggplot(plot_df) + geom_path(mapping = aes(x=x,y=y,color=type))