En publicaciones anteriores he demostrado cómo se pueden consultar los datos del precio de las acciones con, por ejemplo, pandas_datareader en Python.
En esta publicación, presentaré un algoritmo con el que puede construir una cartera eficiente en función de cualquier conjunto de acciones que pueda estar considerando. El algoritmo determinará la participación óptima de cada acción en su cartera, en función del nivel de riesgo que se sienta seguro de asumir.
Más precisamente, presentaré un método para visualizar la frontera eficiente de carteras que consisten en un conjunto específico de acciones. En este ejemplo, trabajaré con las siguientes 8 acciones, que son todas empresas de transporte:
- Yamato Holdings (YATRY)
- Knight-Swift Transportation Holdings (KNX)
- BEST (BEST)
- YRC Worldwide (YRCW)
- Schneider National (SNDR)
- Old Dominion Freight Line (ODFL)
- Arc Best (ARCB)
- Werner Enterprises (WERN)
El riesgo se mide como la desviación estándar de los rendimientos históricos. El rendimiento se mide como el rendimiento diario histórico promedio de las acciones (utilizando los precios de cierre).
Empiezo importando algunos módulos relevantes en Python:
# importar módulos relevantes import pandas as pd import numpy as np import pandas_datareader.data as web import datetime import matplotlib.pyplot as plt import statistics as stat import random as rnd from matplotlib.ticker import StrMethodFormatter
Quiero recopilar datos históricos sobre el precio de las acciones de los 6 meses anteriores. A continuación, especifico la fecha de inicio y finalización del período relevante para recopilar datos:
# especificar la fecha de inicio y finalización relevante para el período de recopilación de datos de precios de acciones start_date = datetime.datetime(2020,4,1) end_date = datetime.datetime(2020,9,30)
A continuación, defino una función auxiliar que tomará un marco de datos de precios de acciones recopilado de Yahoo Finance a través de pandas_datareader y lo traducirá en rendimientos diarios:
# define la función que devuelve una lista de devoluciones diarias
def returns(df):
prices = df["Close"]
returns = [0 if i == 0 else (prices[i]-prices[i-1])/(prices[i-1]) for i in range(0,len(prices))]
return(returns)Ahora defino otra función auxiliar que tomará una lista de ticks de acciones y calculará su rendimiento diario promedio y su desviación estándar de los rendimientos diarios para un período específico. Esta función hace uso de pandas_datareader para consultar datos de precios de acciones de Yahoo:
# definir la función que puede construir un marco de datos con desviaciones estándar y retornos diarios promedio
def analyzeStocks(tickersArr,start_date,end_date):
# crear plantilla de marco de datos vacía
index = ["ticker","return","stdev"]
muArr = []
sigmaArr = []
# recorrer todos los tickers
for i in range(0,len(tickersArr)):
# agregar ticker a la tabla
tick = tickersArr[i]
# obtener datos de precios de acciones
data = web.DataReader(tickersArr[i],"yahoo",start_date,end_date)
# calcular el rendimiento diario promedio
muArr.append(stat.mean(returns(data)))
# calcular la desviación estándar
sigmaArr.append(stat.stdev(returns(data)))
# devolver un marco de datos
return(pd.DataFrame(np.array([tickersArr, muArr, sigmaArr]),index=index,columns=tickersArr))En esta publicación quiero analizar las garrapatas a continuación:
tickersArr = ["YATRY","KNX","BEST","YRCW","SNDR","ODFL","ARCB","WERN"]
Utilizando los tickers anteriores ejecuto analyseStocks para extraer los datos del precio de las acciones y calcular el promedio. rendimiento diario y desviación estándar de los rendimientos diarios:
base_df = analyzeStocks(tickersArr,start_date,end_date) base_df
| YATRY | KNX | BEST | YRCW | SNDR | ODFL | ARCB | WERN | |
|---|---|---|---|---|---|---|---|---|
| ticker | YATRY | KNX | BEST | YRCW | SNDR | ODFL | ARCB | WERN |
| return | 0.004653743523196298 | 0.0023175179239564793 | -0.0034124339485902665 | 0.011159199755783849 | 0.002462051717055063 | 0.003349259316178459 | 0.005861686829084918 | 0.0017903742321965712 |
| stdev | 0.02358463699374274 | 0.02114091659162514 | 0.031397841155750277 | 0.09455276239906354 | 0.019372571935633416 | 0.023305461738410294 | 0.037234069177970675 | 0.02237976138155402 |
Usando matplotlib hago un diagrama de dispersión simple del rendimiento histórico frente al rendimiento de la volatilidad de las acciones individuales:
plt.figure(figsize=(15,8))
muArr = [float(i) for i in base_df.iloc[1,]]
sigmaArr = [float(i) for i in base_df.iloc[2,]]
sharpeArr = [muArr[i]/sigmaArr[i] for i in range(0,len(muArr))]
plt.scatter(sigmaArr,muArr,c=sharpeArr,cmap="plasma")
plt.title("Historical avg. returns vs. standard deviations [single stocks]",size=22)
plt.xlabel("Standard deviation",size=14)
plt.ylabel("Avg. daily return",size=14)Text(0, 0.5, 'Avg. daily return')

Ahora, defino una función de creación de cartera. La función creará un número definido de carteras con pesos asignados aleatoriamente por acción. El rendimiento esperado y la desviación estándar de los rendimientos diarios resultantes de esto se devuelven en forma de un marco de datos de Pandas:
# definir función para crear un número definido de carteras
def portfolioBuilder(n,tickersArr,start_date,end_date):
muArr = []
sigmaArr = []
dailyreturnsArr = []
weightedreturnsArr = []
portfoliodailyreturnsArr = []
# rellenar devoluciones diarias
for i in range(0,len(tickersArr)):
data = web.DataReader(tickersArr[i],"yahoo",start_date,end_date)
dailyreturnsArr.append(returns(data))
# crear n carteras diferentes
for i in range(0,n):
# restablecer la lista de cartera diaria
portfoliodailyreturnsArr = []
# crear peso de cartera
weightsArr = [rnd.uniform(0,1) for i in range(0,len(tickersArr))]
nweightsArr = [i/sum(weightsArr) for i in weightsArr]
# ponderar los retornos diarios
for j in range(0,len(dailyreturnsArr[0])):
temp = 0
for k in range(0,len(tickersArr)):
temp = temp + float(dailyreturnsArr[k][j])*float(nweightsArr[k])
portfoliodailyreturnsArr.append(temp)
# calcular y agregar rendimientos de cartera ponderados diarios mavg
muArr.append(stat.mean(portfoliodailyreturnsArr))
# calcular y agregar la desviación estándar de los rendimientos diarios de la cartera ponderada
sigmaArr.append(stat.stdev(portfoliodailyreturnsArr))
# retorno de los rendimientos esperados y la desviación estándar de las carteras creadas
return([sigmaArr,muArr])Aplico la función de construcción de carteras a los tickers y trazo el resultado usando 500000 carteras aleatorias usando matplotlib.pyplot:
portfoliosArr = portfolioBuilder(500000,tickersArr,start_date,end_date)
plt.figure(figsize=(15,8))
muArr = [float(portfoliosArr[1][i]) for i in range(0,len(portfoliosArr[1]))]
sigmaArr = [float(portfoliosArr[0][i]) for i in range(0,len(portfoliosArr[0]))]
sharpeArr = [muArr[i]/sigmaArr[i] for i in range(0,len(muArr))]
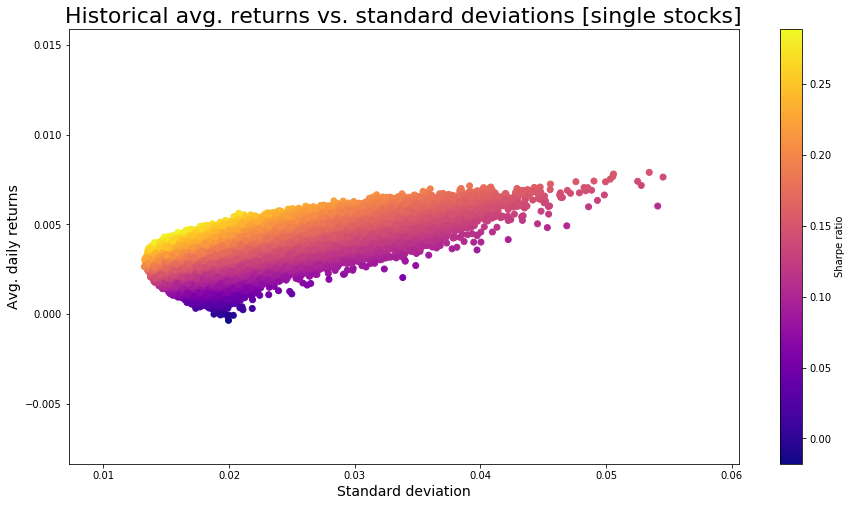
plt.scatter(sigmaArr,muArr,c=sharpeArr,cmap="plasma")
plt.title("Historical avg. returns vs. standard deviations [single stocks]",size=22)
plt.colorbar(label="Sharpe ratio")
plt.xlabel("Standard deviation",size=14)
plt.ylabel("Avg. daily returns",size=14)
Text(0, 0.5, 'Avg. daily returns')

Este gráfico le permite validar si su elección actual de pesos para sus acciones de elección es actualmente eficiente o no. Las carteras eficientes se ubicarían a lo largo de la línea superior del diagrama de dispersión.

Ingeniero industrial especializado en optimización y simulación (R, Python, SQL, VBA)




Leave a Reply