Desarrollar un modelo de simulación simple basado en agentes en Python

En una publicación anterior, demostré cómo visualizar una cuadrícula 2D, usando matplotlib y pyplot en Python (publicación titulada «Visualización de cuadrículas y matrices 2D usando matplotlib en Python»). Esa publicación fue pensada como la primera introducción sobre cómo visualizar cuadrículas en Python. La visualización de cuadrículas puede ser de interés cuando, p. Ej. Visualización de resultados de estudios de simulación basados en agentes. En esta publicación modelé los cimientos de un modelo de simulación simple basado en agentes, utilizando una matriz 2D como entorno que puede ser poblado por dos tipos de agentes. Esta matriz 2D servirá como un campo de batalla en el que dos grupos de agentes pelearán una batalla. Los agentes tienen el mismo conjunto de atributos, uno de ellos es su pertenencia a un grupo. Además de esto, todos tienen una puntuación de vida, que es igual cuando comienza la simulación. Por último, tienen un conjunto de coordenadas (coordenadas xey), que representan su ubicación espacial en un mundo bidimensional. No realizaré un estudio de simulación en esta publicación. Esto se hará en una próxima publicación. Usaré el modelo de esta publicación en una publicación futura para simular una batalla entre los dos grupos de agentes. En el siguiente fragmento de código, defino una clase para agentes, que contiene atributos y métodos relevantes. La documentación se agrega al código en forma de comentarios.

# clase, definiendo agentes como tipos de datos abstractos
class agent:
    # init-method, el método constructor para agentes
    def __init__(self,x,y,group):
        self.life = 100.0 # agent's life score
        self.x = x
        self.y = y
        self.group = group

El siguiente paso es definir una matriz de cuadrícula 2D, en forma de lista 2D. las filas representan coordenadas x, las columnas representan coordenadas y. Esta lista 2D representa el campo de batalla. Lo defino para que tenga un tamaño de 100 x 100 celdas, es decir, 10,000 ubicaciones. Usaré el tipo de lista predeterminado en Python para definir esta matriz de «campo de batalla». El camino a seguir es usar listas de comprensión en Python:

# crear una lista vacía de 100 x 100 usando la comprensión de la lista en Python
battlefield = [[None for i in range(0,100)] for i in range(0,100)]

A continuación, crearé dos grupos de agentes y los ubicaré en ubicaciones aleatorias dentro del campo de batalla. En listas separadas, además, almaceno referencias a los objetos del agente. Crearé 1000 agentes del grupo A y 1000 agentes del grupo B.

# lista con ubicaciones xey disponibles
locations = battlefield.copy() # using .copy prevents copying by reference
# cree una lista vacía para contener referencias de agentes en el futuro, escriba A y B
agents_A = []
agents_B = []
# asignar lugares aleatorios a los agentes del grupo A y B;
# - para esto necesitaré el módulo aleatorio, así que impórtalo
import random
# - definir una función para crear agentes y asignarlos a la cuadrícula
def agentCreator(size,group,groupList,field,n,m):
    # recorrer todo el grupo, es decir, en este caso 1000 unidades
    for j in range(0,size):
        # seleccionar ubicación aleatoria disponible
        while True:
            # coordenada x aleatoria
            x = random.choice(range(0,n))
            # coordenada y aleatoria
            y = random.choice(range(0,m))
            # comprobar si hay espacio disponible; si no, repita
            if field[x][y] == None:
                field[x][y] = agent(x=x,y=y,group=group)
                # agregar la referencia del objeto del agente a la lista de grupos
                groupList.append(field[x][y])
                # salir mientras bucle; se toma el lugar en el campo
                break
# -- puedo poblar el campo de batalla usando la función agentCreator
agentCreator(size = 1000,
                group = "A",
                groupList = agents_A,
                field = battlefield,
                n = 100,
                m = 100)
 agentCreator(size = 1000,
                group = "B",
                groupList = agents_B,
                field = battlefield,
                n = 100,
                m = 100)

La lista 2D «campo de batalla» ahora contiene «Ninguno» o referencias de agentes, de tipo A o B. Todos los agentes tienen una puntuación de vida de 100, ya que la batalla aún no ha comenzado.

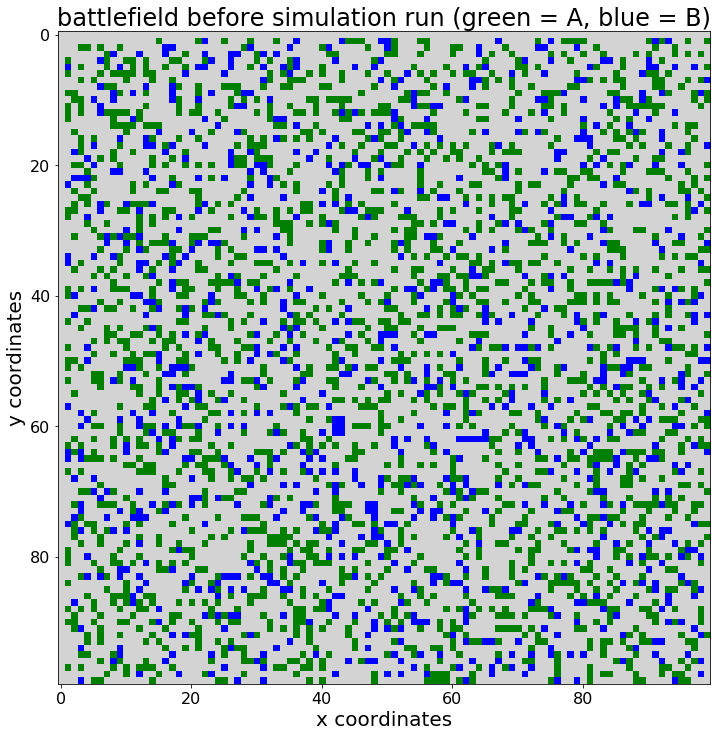
Para completar esta primera publicación sobre la simulación basada en agentes, visualizaré la ubicación de los agentes de tipo A y la ubicación de los agentes de tipo B, en dos diagramas de cuadrícula separados. La clave para hacer esto es usar matplotlib.pyplot, con el método .imshow ():

# .imshow () necesita una matriz con elementos flotantes;
population = [[0.0 for i in range(0,100)] for i in range(0,100)]
# si el agente es de tipo A, poner 1.0, si es de tipo B, pyt 2.0
for i in range(1,100):
    for j in range(1,100):
        if battlefield[i][j] == None: # vacía
            pass # dejar 0.0 en la celda de población
        elif battlefield[i][j].group == "A": # agentes del grupo A
            population[i][j] = 1.0 # 1.0 signifa"A"
        else: # group B agents
            population[i][j] = 2.0 # 2.0 signifa"B"
# importar pyplot y colores de matplotlib
from matplotlib import pyplot, colors
# usando colores de matplotlib, defina un mapa de color
colormap = colors.ListedColormap(["lightgrey","green","blue"])
# definir el tamaño de la figura usando pyplot
pyplot.figure(figsize = (12,12))
# usando pyplot agregue un título
pyplot.title("battlefield before simulation run (green = A, blue = B)",
            fontsize = 24)
# usando pyplot agregue etiquetas xey
pyplot.xlabel("x coordinates", fontsize = 20)
pyplot.ylabel("y coordinates", fontsize = 20)
# ajustar las marcas de los ejes xey, usando pyplot
pyplot.xticks(fontsize = 16)
pyplot.yticks(fontsize = 16)
# use el método .imshow () de pyplot para visualizar las ubicaciones de los agentes
pyplot.imshow(X = population,
             cmap = colormap)

<matplotlib.image.AxesImage at 0x1c756b04c88>

En una próxima publicación utilizaré el modelo básico desarrollado en esta publicación para simular la batalla real entre los dos grupos de agentes. Veremos diferentes parámetros y cómo influyen en el resultado de la batalla. Este será nuestro punto de partida para aprender más sobre la simulación basada en agentes en Python.