Programación lineal multiobjetivo con subproblemas ponderados, usando PuLP en Python

En la publicación más reciente sobre programación lineal, se utilizó PuLP para resolver el siguiente problema de optimización lineal, utilizando dos enfoques. El enfoque n. ° 1 se basó en resolver un subproblema con un solo objetivo primero, luego agregando el resultado óptimo de ese problema a un segundo subproblema que se consideraba el objetivo dos únicamente. El enfoque n. ° 2 se basa en combinar todos los objetivos en una función objetivo general, combinando objetivos individuales con pesos escalares.

En esta publicación, se muestra un enfoque alternativo para resolver el siguiente problema de programación lineal multiobjetivo: se utiliza el enfoque n. ° 1, pero aplicaré pesos en su lugar:

El enfoque que utilizo ahora es resolver el problema en dos pasos, donde un subproblema con un solo objetivo se resuelve primero y su resultado óptimo se agrega a un segundo subproblema con solo el segundo objetivo como restricción. Este enfoque ha sido demostrado antes, pero esta vez aplicaré un factor de peso escalar a esa restricción, considerando el resultado óptimo del subproblema con 0-100%.

Partiendo del primer objetivo, el primer subproblema a resolver sería el siguiente:

El valor objetivo óptimo para el subproblema anterior es 30.

Después de haber resuelto el primer subproblema, el segundo objetivo sería considerado por un segundo subproblema agregando el resultado óptimo al problema anterior como una restricción ponderada:

Aquí está la implementación en Python, usando el módulo PuLP y aplicando un tamaño de paso de 0.01:

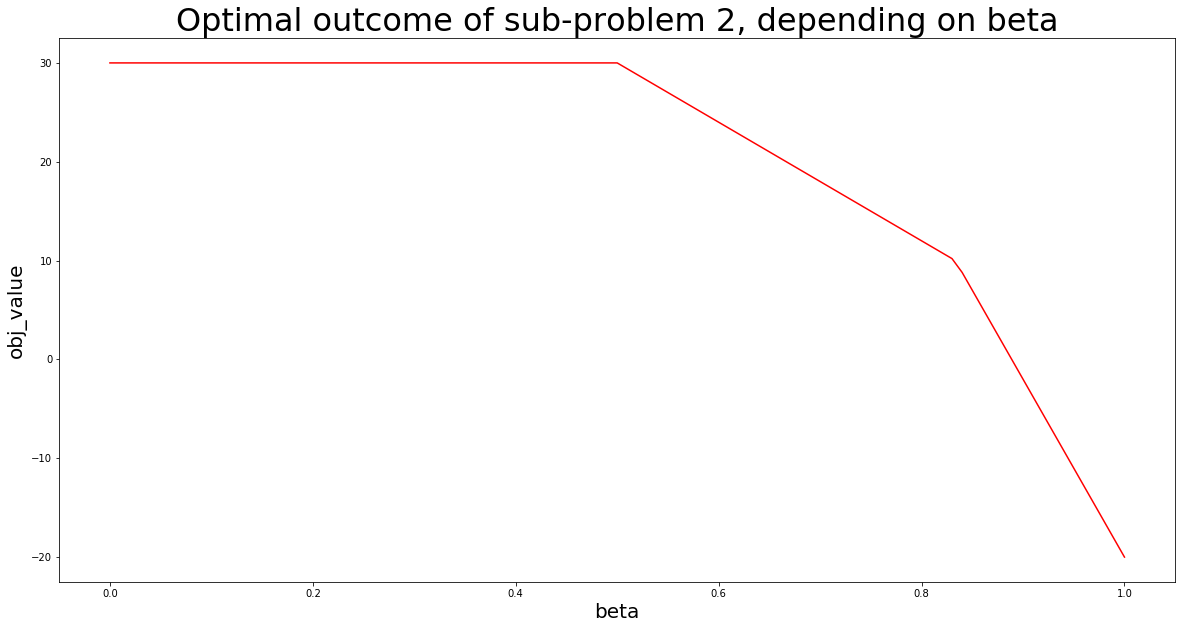
# importar PuLP para modelar y resolver problemas
import pulp

# import matplotlib.pyplot para visualización
import matplotlib.pyplot as plt 

# importar pandas y numpy para poder almacenar soluciones en DataFrame
import numpy as np
import pandas as pd

# definir tamaño de paso
stepSize = 0.01

# inicializar DataFrame vacío para almacenar resultados de optimización
solutionTable = pd.DataFrame (columnas = ["beta", "x1_opt", "x2_opt", "obj_value"])

# declarar variables de optimización usando PuLP y LpVariable
x1 = pulp.LpVariable ("x1", lowBound = 0)
x2 = pulp.LpVariable ("x2", lowBound = 0)

# modelar y resolver el subproblema núm. 1
linearProblem = pulp.LpProblem ("Primer subproblema", pulp.LpMaximize)
linearProblem + = 2 * x1 + 3 * x2 # agregar objetivo no. 1
linearProblem + = x1 + x2 <= 10 # agregar restricciones del enunciado original del problema
linearProblem + = 2 * x1 + x2 <= 15
solution = linearProblem.solve ()

# almacenar el resultado óptimo del subproblema núm. 1 en variable
OptimObj1 = pulp.value (linearProblem.objective)

# iterar a través de los valores beta de 0 a 1 con stepSize y escribir soluciones PuLP en solutionTable
for i in range(0,101, int (stepSize * 100)):
        # declarar el problema de nuevo
        linearProblem = pulp.LpProblem ("Maximización lineal multiobjetivo", pulp.LpMaximize)
        # agregue el segundo objetivo como función objetivo a este subproblema
        linearProblem + = 4 * x1-2 * x2
        # agregue las restricciones del enunciado original del problema
        linearProblem + = x1 + x2 <= 10
        linearProblem + = 2 * x1 + x2 <= 15
        # agregar una restricción adicional en el nivel beta, considerando el resultado óptimo del subproblema núm. 1
        linearProblem + = 2 * x1 + 3 * x2> = (i / 100) * óptimoObj1
        # resolver el problema
        solution = linearProblem.solve ()
        # escribir soluciones en DataFrame
        solutionTable.loc [int (i / (stepSize * 100))] = [i / 100,
                                                     pulp.value(x1),
                                                     pulp.value(x2),
                                                     pulp.value(linearProblem.objective)]

# visualizar el resultado de la optimización, usando matplotlib.pyplot
# - establecer el tamaño de la figura
plt.figure (figsize = (20,10))
# - crear diagrama de línea
plt.plot (solutionTable ["beta"], solutionTable ["obj_value"], color = "red")
# - agregar etiquetas de eje
plt.xlabel ("beta", size = 20)
plt.ylabel ("obj_value", size = 20)
# - agregar título de la trama
plt.title ("Resultado óptimo del subproblema 2, según beta", size = 32)
# - mostrar trama
plt.show ()

Los resultados indican que existe un rango para beta en el que un aumento en beta no afectará el resultado óptimo del subproblema 2, es decir, no afectará al objetivo 2.