Pronóstico de salida con promedio móvil

En una publicación anterior expliqué el pronóstico basado en CAGR. El pronóstico basado en CAGR es un método de pronóstico muy simple que a menudo se aplica en la industria, por ejemplo, para pronosticar ventas y producción.

Los modelos de pronóstico simples tienen beneficios. Son fáciles de entender y fáciles de implementar. Además, contienen pocos parámetros y, por lo tanto, son muy precisos en sus supuestos centrales. De esta manera se puede decir que los métodos de pronóstico simples son en muchos casos los mejores métodos de pronóstico. En otras palabras: si intenta predecir el futuro, es posible que desee hacerlo con un modelo de pronóstico que comprenda completamente y que pueda explicar a cualquier persona en cualquier momento.

En esta publicación, me gustaría presentar el pronóstico de series de tiempo basado en un cálculo simple de promedio móvil. Los promedios móviles, también conocidos como promedios móviles o medios móviles, se utilizan para analizar y preprocesar datos de series temporales históricas. Sin embargo, pueden usarse para crear un algoritmo de pronóstico simple.

Distingo el pronóstico de promedio móvil simple en dos categorías:

(a) pronósticos a partir de datos históricos mediante el cálculo de un promedio móvil

(b) igual que (a), pero con un parámetro de crecimiento intrínseco adicional

La categoría (b) es, por lo tanto, una combinación de pronósticos basados en CAGR y pronósticos de promedio móvil.

Al igual que el pronóstico basado en CAGR, el pronóstico de promedio móvil simple solo puede usarse para horizontes de tiempo límite.

Implemento un enfoque de pronóstico de este tipo en el ejemplo de codificación a continuación, usando una función que calcula un promedio móvil de longitud definida. Implemento esta función en R y la aplico para pronosticar valores futuros. Llamo a la función «sma_forecast». Se implementa en el código R a continuación:

sma_forecast = function(past,length){
  
  future = rep(0,times = length)
  
  prediction = c(past,future)
  
  for(i in (length(past)+1):length(prediction)){
    prediction[i] = mean(prediction[(i-length(past)):(i-1)])
  }
  
  return(prediction)
}

El siguiente paso en este flujo de trabajo es leer datos históricos. En este caso, leo datos sobre la producción anual de la industria automotriz por país, medidos en número de unidades producidas en un año determinado dentro de un país determinado. El último paso es calcular el pronóstico, usando el sma_forecast. Todo esto se hace en el siguiente ejemplo de codificación, usando R:

library(readxl)

data_df = as.data.frame(read_xls("oica.xls"))

head(data_df)

##   year   country    total
## 1 2018 Argentina   466649
## 2 2018   Austria   164900
## 3 2018   Belgium   308493
## 4 2018    Brazil  2879809
## 5 2018    Canada  2020840
## 6 2018     China 27809196

tail(data_df)

##     year    country    total
## 835 1999     Turkey   297862
## 836 1999    Ukraine     1918
## 837 1999         UK  1973519
## 838 1999        USA 13024978
## 839 1999 Uzbekistan    44433
## 840 1999     Others    11965

library(dplyr)
data_df = filter(data_df,country=="USA")

library(ggplot2)
ggplot(data_df) + 
  geom_path(mapping = aes(x = year, y = total/1000000), 
            size = 2, 
color = "red") + 
  labs(title = "US automotive industry production output",
       subtitle = "historical OICA data, for 1999 - 2018") +
  xlab("year") +
  ylab("output [millions of units]") + 
  ylim(0,15)

library(dplyr)
data_df = data_df %>% arrange(desc(-year))

predictionVals = sma_forecast(past=data_df$total,length = 10)

plot_df = as.data.frame(matrix(nrow=length(predictionVals),ncol= 4))
colnames(plot_df) = c("year","country","total","category")
plot_df$total = predictionVals
plot_df$category[1:nrow(data_df)] = "history"
plot_df$category[(nrow(data_df)+1):length(predictionVals)] = "prediction"
plot_df$year = data_df$year[1]:(data_df$year[1]+length(predictionVals)-1)
plot_df$country = data_df$country[1]

ggplot(plot_df) +
  geom_point(mapping = aes(x = year,
                          y = total/1000000,
                          color = category),
             size = 2) +
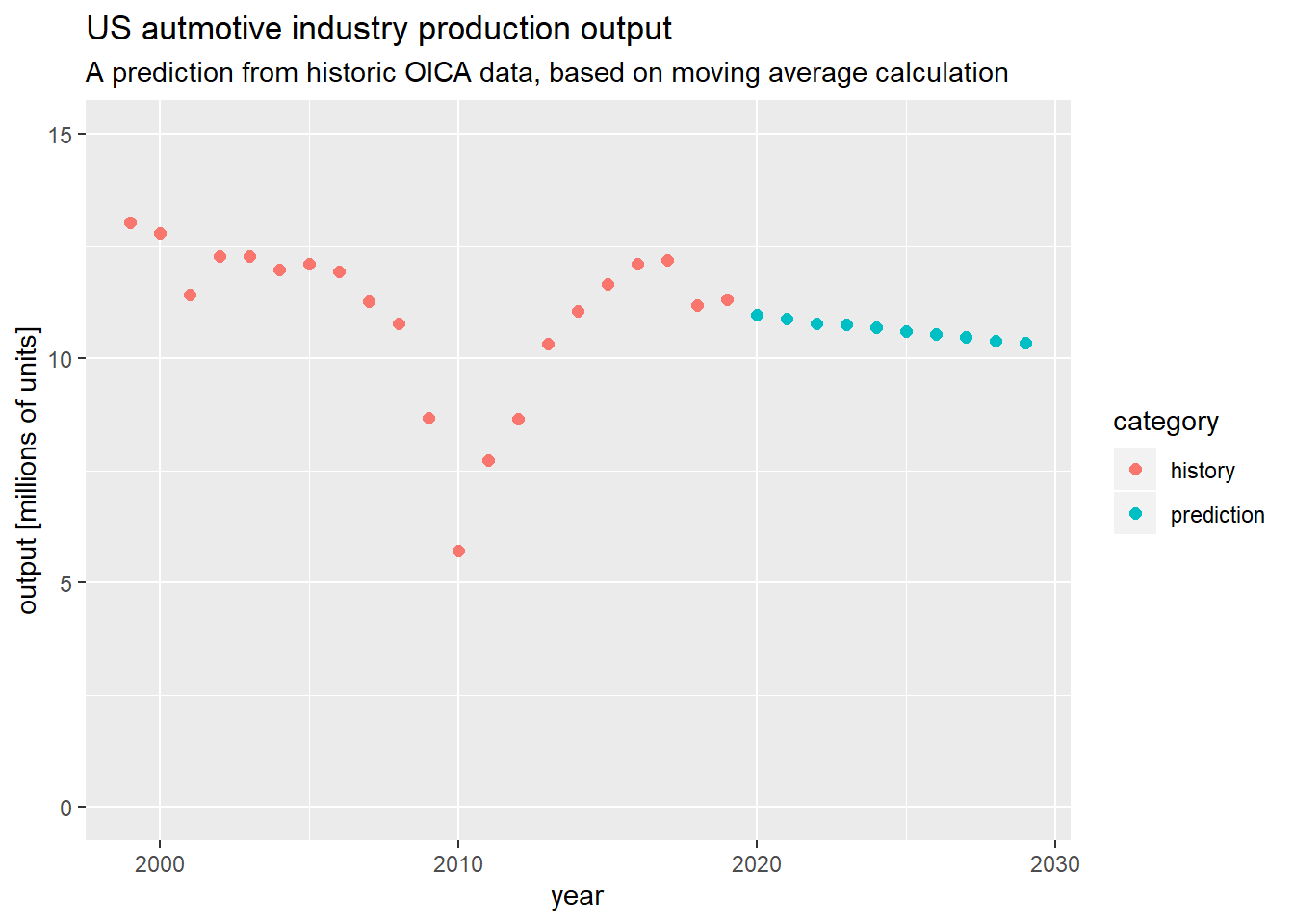
  labs(title = "US autmotive industry production output",
       subtitle = "A prediction from historic OICA data, based on moving average calculation") +
  xlab("year") +
  ylab("output [millions of units]") +
  ylim(0,15)

Termino mi ejemplo en este punto.

Cosas que podría haber añadido:

(a) División en el entrenamiento y el conjunto de prueba para evaluar el método.

(b) Método de evaluación para varios países, intervalos de tiempo y duración de las predicciones

(d) …

Si esta publicación le pareció interesante, puede considerar revisar mis otras publicaciones, por ejemplo, pronósticos basados en CAGR, obtención y análisis de datos OICA, análisis de series temporales, programación lineal, fuentes públicas de datos de ventas de la industria automotriz, etc.