Solución de un problema de programación lineal utilizando la librería lpSolve en R

En esta publicación, se muestra cómo resolver un problema de programación lineal utilizando el lenguaje R. También puedes encontrar otras publicaciones en este blog que analizan otras tareas de optimización lineal, como el problema de transporte (resuelto con lp.transport en R), el problema de asignación (resuelto con lp.assign en R) y programación lineal de enteros (también se pueden resolver problemas de enteros mixtos lineales en R).

La programación lineal se aplica ampliamente para modelar distintos tipos de problemas como los de ubicación de instalaciones, asignación de recursos, transporte, redes, entre otros. lpSolve es una librería disponible en R que brinda acceso a una interfaz basada en C para resolver problemas de programación lineal. Dado que la interfaz está desarrollada en C, tiene el máximo rendimiento, minimizando el tiempo requerido para resolver problemas de programación lineal sin tener que cambiar el entorno de programación o el lenguaje de programación.

En esta publicación se muestra un ejemplo de un problema de programación lineal resuelto con lpSolve. La función objetivo busca maximizar los ingresos definidos por la función f (x, y) = 2x + 3y, sujeta a las restricciones donde x, y son variables no negativas; x + y son valores no mayores que 3.

Este problema es fácil de resolver trazando una gráfica de línea o aplicando el algoritmo simplex. No se explica aquí a detalle los algoritmos o metodología para la resolución de problemas lineales, pero mostramos un breve ejemplo de cómo se puede modelar y resolver este simple problema usando lpSolve en R. Luego, podrá apreciar una ilustración gráfica que verifica el resultado.

Primero, cargamos el paquete lpSolve (previa instalación) y el modelo del problema, usando la API lpSolve:

library(lpSolve)
f.obj <- c(2,3)                           # vector de coeficiente de la función objetivo
f.con <- matrix(c(1,1),nrow=1,byrow=TRUE) # matriz de coeficientes para la matriz de restricciones
f.dir <- c("<=")                          # vector de dirección de la restricción
f.rhs <- c(3)                             # valores de la restricción

Ahora se resolvemos el problema lineal:

solution <- lp("max",f.obj,f.con,f.dir,f.rhs)
solution

## Success: the objective function is 9

La solución óptima es la siguiente (valor óptimo de x, y):

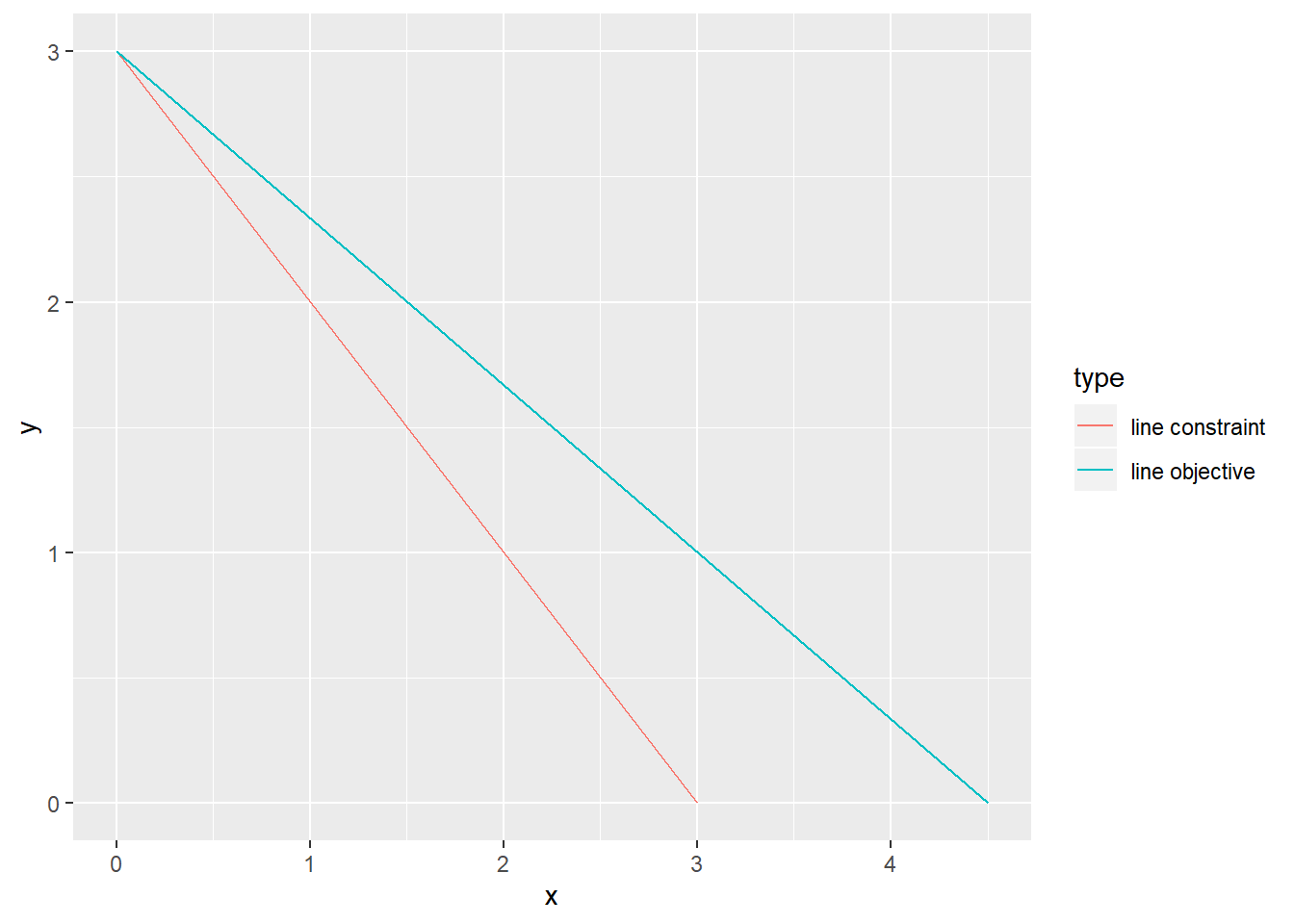
solution$solution

## [1] 0 3

Finalmente, procedemos a verificar gráficamente el resultado. Se definen dos líneas que se visualizan usando geom_line del paquete ggplot2. La primera línea representa la restricción que x + y no debe ser mayor que 3, la segunda línea representa la función objetivo. La línea de la función objetivo representa su valor máximo alcanzable, es decir, el valor óptimo. La línea de la restricción representa sus casos vinculantes, es decir, cuando es exactamente igual a 3. En términos más simples: «objetivo de línea»: 2x + 3y = 9 «restricción de línea»: x + y = 3

library(ggplot2)
plot_df <- as.data.frame(matrix(nrow=4,ncol=3))
colnames(plot_df) <- c("x","y","type")
plot_df$x <- c(0,3,0,9/2)
plot_df$y <- c(3,0,9/3,0)
plot_df$type <- c("line constraint","line constraint", "line objective", "line objective")
ggplot(plot_df) + geom_path(mapping = aes(x=x,y=y,color=type))

Considerando que x + y = 3, podemos observar que la solución óptima a este problema debe ser x = 0, y = 3; y que estos valores maximizan la función objetivo

Si está interesado en temas como programación no lineal (por ejemplo, el descenso de gradiente con nloptr) o la optimización cuadrática (quadprog) en R, te invitamos a consultar estas publicaciones de este blog:

Editado y traducido por: Ricardo Caballero, M.Sc.
Revisado por: Oswaldo Almonacid