이 게시물에서는 SciPy를 사용하여 모델링하는 방법과 선형 최적화 문제를 보여줍니다:
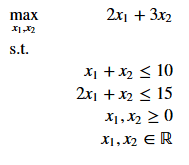
Python의 SciPy-package에서 linprog 함수를 사용하여이 간단한 선형 최적화 문제를 모델링하고 해결할 수 있습니다. 이를 위해 벡터 행렬 표기법 형식으로 설명하고 최소화 문제로 변환합니다.

이제이 문제를 해결할 수 있습니다 :
# 비용 함수 계수 값으로 비용리스트 설정
c = [-2,-3]
# 구속 계수 행렬 A_ub 설정
A_ub = [[1,1],
[2,1]]
# 상한에 대한 제한 목록 (제약 제한 이하)
b_ub =[10,15]
# 또한 각 최적화 변수에 대한 경계 튜플을 준비하고 목록을 요약해야합니다
x1_bounds = (0,None)
x2_bounds = (0,None)
# 이제 SciPy.optimize.linprog를 사용하여 현재 문제를 모델링하고 해결합니다.
from scipy.optimize import linprog
model_linear = linprog(c=c,
A_ub=A_ub,
b_ub = b_ub,
bounds = [x1_bounds,x2_bounds])
# 인쇄 솔루션
print(str(model_linear))
fun: -30.0
message: 'Optimization terminated successfully.'
nit: 1
slack: array([ 0., 5.])
status: 0
success: True
x: array([ 0., 10.])
최적의 솔루션은 (x1 = 0; x2 = 30)입니다.
최적의 솔루션 값은 30입니다.
첫 번째 제약 조건은 바인딩입니다.
두 번째 제약 조건은 구속력이 없습니다.

최적화 및 시뮬레이션을 전문으로하는 산업 엔지니어 (R, Python, SQL, VBA)





Leave a Reply