R에서 lpSolve를 사용한 수학적 솔루션 방법

이 게시물에서는 R에서 간단한 선형 최적화를 수행하는 방법을 보여줍니다. 운송 문제(lp.transport로 해결할 수 있음), 할당 문제( lp.assign으로 풀 수 있음) 및 정수 선형 프로그래밍(선형 혼합 정수 문제도 R에서 풀 수 있음).

선형 프로그래밍은 시설 위치 문제를 모델링하는 데 널리 적용됩니다. lpSolve는 선형 프로그래밍 문제를 해결하기 위해 C 기반 인터페이스에 대한 액세스를 제공하는 R에서 사용할 수 있는 확장입니다. 인터페이스가 C로 개발되었기 때문에 프로그래밍 환경이나 프로그래밍 언어를 전환할 필요 없이 선형 프로그래밍 문제를 해결하는 데 필요한 시간을 최소화하여 최대 성능을 제공합니다.

이 게시물에서는 lpSolve로 해결된 간단한 선형 프로그래밍 문제의 예를 제공합니다.

목적 함수는 x, y가 음수가 아니고 x + y가 3보다 크지 않다는 제약 조건에 따라 함수 f(x,y) = 2x + 3y로 정의된 수익을 최대화하는 것입니다.

인터넷에서 알 수 있듯이 이 문제는 쉽게 해결할 수 있습니다. 예를 들어 선 그림을 그리거나 심플렉스 알고리즘을 적용하면 됩니다. 선형 문제를 해결하기 위한 알고리즘이나 방법론을 자세히 설명하지는 않겠지만 R의 lpSolve를 사용하여 이 간단한 문제를 모델링하고 해결하는 방법에 대한 간단한 예를 제공할 것입니다. 그 다음에는 결과를 확인하는 그래픽 그림을 보여드리겠습니다.

lpSolve 패키지(이미 설치되어 있음)를 로드하고 lpSolve API를 사용하여 문제를 모델링합니다.

library(lpSolve)
f.obj <- c(2,3)                           # coefficient vector of objective function
f.con <- matrix(c(1,1),nrow=1,byrow=TRUE) # coefficient matrix for constraint matrix
f.dir <- c("<=")                          # constraint direction vector
f.rhs <- c(3)                             # constraint values

이제 선형 문제를 해결해 보겠습니다.

solution <- lp("max",f.obj,f.con,f.dir,f.rhs)
solution

## Success: the objective function is 9

최적의 솔루션은 다음과 같습니다(당면한 문제에 대한 최적의 x 및 y 값).

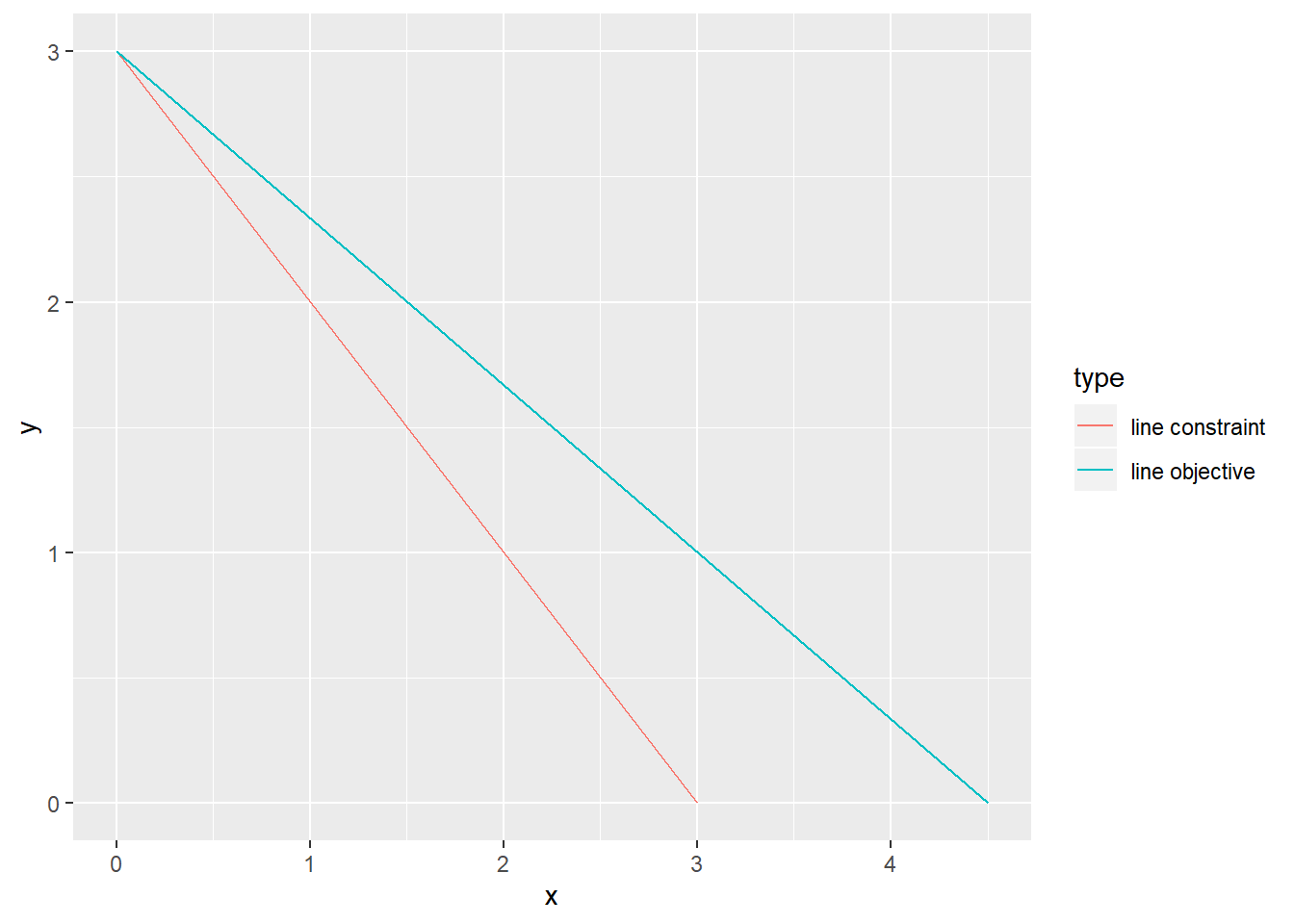
solution$solution

## [1] 0 3

이제 결과를 그래픽으로 확인하겠습니다. ggplot2 패키지의 geom_line을 사용하여 시각화하는 두 줄을 정의합니다. 첫 번째 줄은 x + y가 3보다 크지 않아야 한다는 제약 조건을 나타내고 두 번째 줄은 목적 함수를 나타냅니다. 목적 함수의 선은 달성 가능한 최대값, 즉 최적값을 나타냅니다. 제약 조건에 대한 라인은 바인딩 케이스를 나타냅니다. 즉, 정확히 3일 때입니다. 더 간단한 용어로: “라인 목표”: 2x + 3y = 9 “라인 제약 조건”: x + y = 3

library(ggplot2)
plot_df <- as.data.frame(matrix(nrow=4,ncol=3))
colnames(plot_df) <- c("x","y","type")
plot_df$x <- c(0,3,0,9/2)
plot_df$y <- c(3,0,9/3,0)
plot_df$type <- c("line constraint","line constraint", "line objective", "line objective")
ggplot(plot_df) + geom_path(mapping = aes(x=x,y=y,color=type))