Otimização linear multiobjetivo com subproblemas ponderados, usando PuLP em Python

No meu post mais recente sobre programação linear, apliquei o PuLP para resolver o problema de otimização abaixo do linear, usando duas abordagens. A abordagem nº 1 foi baseada na resolução de um subproblema com apenas um objetivo primeiro e, em seguida, adicionar o resultado ideal desse problema a um segundo subproblema que considerava apenas o objetivo dois. A abordagem nº 2 é baseada na combinação de todos os objetivos em uma função objetivo geral, combinando objetivos únicos com pesos escalares.

Neste post, quero mostrar uma abordagem alternativa para resolver o problema de otimização linear multiobjetivo abaixo: usarei a abordagem nº 1, mas aplicarei pesos:

A abordagem que uso agora é resolver o problema em duas etapas, onde um subproblema com apenas um objetivo é resolvido primeiro e seu resultado ideal é adicionado a um segundo subproblema com apenas o segundo objetivo como restrição. Essa abordagem já foi demonstrada anteriormente, mas desta vez aplicarei um fator de peso escalar a essa restrição, considerando o resultado ideal do subproblema com 0-100%.

Começando com o primeiro objetivo, o primeiro subproblema a resolver seria o seguinte:

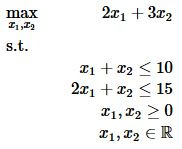
O valor objetivo ideal para o subproblema acima é 30.

Depois de ter resolvido o primeiro subproblema, o segundo objetivo seria considerado por um segundo subproblema adicionando o resultado ideal ao problema acima como uma restrição ponderada:

Aqui está a implementação em Python, usando o módulo PuLP e aplicando um step-size de 0,01:

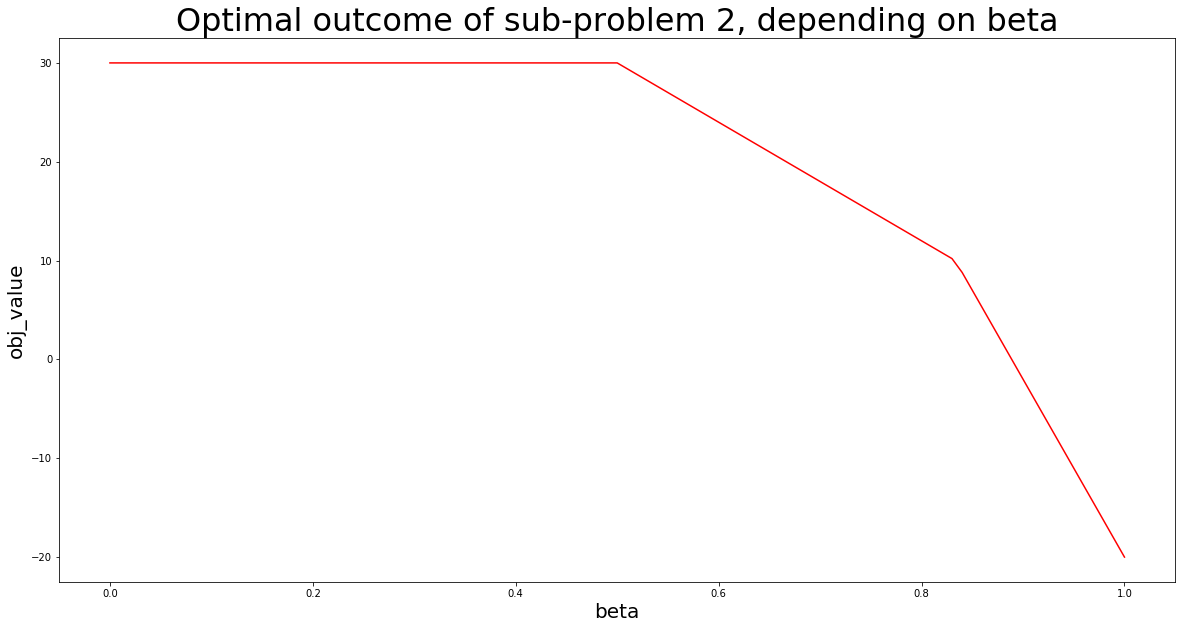
# importar PuLP para modelagem e resolução de problemas
import PuLP

# importa matplotlib.pyplot para visualização
import matplotlib.pyplot as plt 

# importa pandas e numpy para poder armazenar soluções em DataFrame
import numpy as np
import pandas as pd

# define o tamanho do passo
stepSize = 0.01

# inicializa DataFrame vazio para armazenar resultados de otimização
solutionTable = pd.DataFrame(columns=["beta","x1_opt","x2_opt","obj_value"])

# declara variáveis de otimização usando PuLP e LpVariable
x1 = PuLP.LpVariable("x1",lowBound=0)
x2 = PuLP.LpVariable("x2",lowBound=0)

# modelar e resolver o subproblema no. 1
linearProblem = PuLP.LpProblem("First sub-problem",PuLP.LpMaximize)
linearProblem += 2*x1 + 3*x2 # adicionar objetivo no. 1
linearProblem += x1 + x2 <= 10 # adiciona restrições da declaração do problema original
linearProblem += 2*x1 + x2 <= 15
solution = linearProblem.solve()

# armazena o resultado ideal do subproblema no. 1 em variável
optimalObj1 = PuLP.value(linearProblem.objective)

# iterar os valores beta de 0 a 1 com stepSize e gravar soluções PuLP em solutionTable
for i in range(0,101,int(stepSize*100)):
        # declara o problema novamente
        linearProblem = PuLP.LpProblem("Multi-objective linear maximization",PuLP.LpMaximize)
        # adicione o segundo objetivo como função objetivo a este subproblema
        linearProblem += 4*x1-2*x2
        # adiciona as restrições da declaração do problema original
        linearProblem += x1 + x2 <= 10
        linearProblem += 2*x1 + x2 <= 15
        # adicionar restrição adicional no nível beta, considerando o resultado ideal do subproblema no. 1
        linearProblem += 2*x1 + 3*x2 >= (i/100)*optimalObj1
        # resolva o problema
        solution = linearProblem.solve()
        # escreve soluções no DataFrame
        solutionTable.loc[int(i/(stepSize*100))] = [i/100,
                                                     PuLP.value(x1),
                                                     PuLP.value(x2),
                                                     PuLP.value(linearProblem.objective)]

# visualize o resultado da otimização, usando matplotlib.pyplot
# -- define o tamanho da figura
plt.figure(figsize=(20,10))
# -- cria um gráfico de linha
plt.plot(solutionTable["beta"],solutionTable["obj_value"],color="red")
# -- adiciona rótulos de eixo
plt.xlabel("beta",size=20)
plt.ylabel("obj_value",size=20)
# -- adiciona o título do gráfico
plt.title("Optimal outcome of sub-problem 2, depending on beta",size=32)
# -- mostra o enredo
plt.show()

Os resultados indicam que existe algum intervalo para beta onde um aumento no beta não afetará o resultado ideal do subproblema 2, ou seja, não afetará o objetivo 2.