Neste artigo, forneço vários exemplos de regressão em R. Comparo vários métodos de regressão usando R. Os métodos que apresentarei são regressão linear simples, regressão linear múltipla, regressão polinomial, regressão de árvore de decisão e regressão de máquina de vetor de suporte.
Pacotes necessários para regressão em R
Começo carregando os pacotes necessários (além da biblioteca base do R):
library(dplyr) # package for data wranglinglibrary(ggplot2) # package for data visualization
library(rpart) # package for decision tree regression analysis
library(randomForest) # package for random forest regression analysislibrary(e1071) # package for support vector regression analysis
library(caTools) # package for e.g. splitting into training and test setsLendo os dados antes da regressão em R
Agora leio dados que usarei para implementar meus exemplos de regressão em R. Os dados contêm dados sobre produto interno bruto, investimentos privados brutos, expectativa de vida, tamanho da população e investimentos em pesquisa e desenvolvimento.
# reading in gross domestic product data
gdp_df <- read.csv("gross domestic product.csv",header=TRUE)
# reading in gross private investment data
investment_df <- read.csv("gross private investments.csv",header=TRUE)
# reading in life expectancy data
lifeexpectancy_df <- read.csv("life expectancy.csv",header=TRUE)
# reading in population data
population_df <- read.csv("population.csv",header=TRUE)
# reading in research and development data
rnd_df <- read.csv("research and development.csv",header=TRUE)
# joining all data into a final input data set
data_df <- gdp_df %>% inner_join(investment_df,by="DATE",fa) %>%
inner_join(lifeexpectancy_df,by="DATE") %>%
inner_join(population_df,by="DATE") %>%
inner_join(rnd_df,by="DATE")
# rename column headers
colnames(data_df) <-c("date",
"gdp",
"private_investment",
"life_expectancy",
"population",
"rnd")
# convert date entries from characters into date data types
data_df$date <- as.Date(data_df$date)Como primeiro passo, quero visualizar os dados. Para permitir uma comparação visual aprimorada das tendências de crescimento nos dados, eu os normalizo. Para isso defino uma função:
normalize_data <- function(x){
return ((x-min(x))/(max(x)-min(x)))
}Usando a função, converto meu data_df em um quadro de dados compatível com ggplot que é normalizado. Eu alimento isso para o ggplot e visualizo os dados:
dates <- c(data_df$date,
data_df$date,
data_df$date,
data_df$date,
data_df$date)
values <- c(normalize_data(data_df$gdp),
normalize_data(data_df$private_investment),
normalize_data(data_df$life_expectancy),
normalize_data(data_df$population),
normalize_data(data_df$rnd))
sources <- c(rep("gdp",times=nrow(data_df)),
rep("private_investment",times=nrow(data_df)),
rep("life_expectancy",times=nrow(data_df)),
rep("population",times=nrow(data_df)),
rep("rnd",times=nrow(data_df)))
# build ggplot-friendly data frame
ggdata_df <- as.data.frame(matrix(nrow=5*nrow(data_df),ncol=3))
colnames(ggdata_df) <- c("date","value","source")
# populating the ggplot-friendly data frame
ggdata_df$date <- as.Date(dates)
ggdata_df$value <- as.numeric(values)
ggdata_df$source <- sources
# visualize the normalized values (i.e. data set) with ggplot
ggplot(ggdata_df) +
geom_point(mapping = aes(x=dates,y=values,color=sources)) +
ggtitle("Normalized data set values; time-series view") +
xlab("Time") +
ylab("Normalized observation values")
Pipeline para regressão em r
Depois de visualizar o conjunto de dados de interesse, testo vários modelos de regressão diferentes nos dados.
Para cada abordagem alternativa de regressão em R, o processo é sempre o mesmo:
- Divida os dados em conjunto de treinamento e teste
- Treine um preditor no conjunto de treinamento
- Revise a qualidade do ajuste para o regressor com base no conjunto de treinamento
- Regressor de teste no conjunto de teste
Regressão linear simples em R
Vou começar minha série de exemplos sobre regressão em R com um modelo de regressão linear simples. Eu tento prever o tamanho da população a partir de outros dados de observação fornecidos pelo conjunto de dados.
Abaixo implemento o pipeline mencionado acima (observe que não preciso normalizar os dados neste caso).
Como o tamanho da população servirá como variável dependente, agora tenho quatro variáveis independentes para escolher. Para este exemplo, escolhi a expectativa de vida (ao nascer) como variável independente de previsão. Ou seja, para o meu exemplo de regressão em RI, neste caso, derivará a relação linear entre o tamanho da população e a expectativa de vida.
Minha suposição é que maior expectativa de vida acompanha maior tamanho da população (para o mesmo país e região).
# randomly generate split
set.seed(123)
training_split <- sample.split(data_df$date,SplitRatio = 0.8)
# extract training and test sets
training_df <- subset(data_df, training_split)
test_df <- subset(data_df, !training_split)
# train predictor based on training set
predictor <- lm(formula = population ~ life_expectancy, data=training_df)
# print summary of simple linear regression
summary(predictor)##
## Call:
## lm(formula = population ~ life_expectancy, data = training_df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -15279 -6746 1131 4625 17762
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -840396.8 32055.5 -26.22 <2e-16 ***
## life_expectancy 14629.9 427.4 34.23 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 8377 on 44 degrees of freedom
## Multiple R-squared: 0.9638, Adjusted R-squared: 0.963
## F-statistic: 1172 on 1 and 44 DF, p-value: < 2.2e-16Visualizo o resultado dessa regressão em R usando ggplot2. No código abaixo eu mostro como fazer isso:
ggplot(training_df) +
geom_point(mapping=aes(x=life_expectancy,
y=population)) +
geom_line(mapping=aes(x=life_expectancy,
y=predict(predictor,training_df)),color="red") +
ggtitle("Population in dependence of life expectancy; linear regression (training)") +
xlab("US life expectancy since birth [years]") +
ylab("US population size [-]")
Também quero ver um histograma dos resíduos de previsão:
hist(predictor$residuals,
main ="Histogram of model residuals",
xlab="Model residuals [-]")
Além disso, quero ver os resíduos em função da previsão do tamanho da observação variável:
plot(x=training_df$life_expectancy,
y=predictor$residuals,
main = "Model residuals in dependence of independent variable",
xlab="US life expectancy [years]",
ylab="Model residuals [-]")
Isso parece um viés um tanto sistemático. Também posso tentar mostrar isso em um gráfico qqnorm:
qqnorm(predictor$residuals)
Depois de treinar o preditor linear, testo o desempenho da previsão no conjunto de teste:
# predict the test set values
predictions <- predict(predictor,test_df)
# visualize prediction accuracy
ggplot(test_df) +
geom_point(mapping=aes(x=life_expectancy,y=population)) +
geom_line(mapping=aes(x=life_expectancy,predictions),color="red") +
ggtitle("Population in dependence of life expectancy; linear regression (test)") +
xlab("US life expectancy since birth [years]") +
ylab("US population size [-]")
Vamos ver se podemos obter previsões mais precisas usando uma abordagem de regressão linear multivariada. Mas primeiro, armazenamos as previsões de regressão linear simples para todo o conjunto de dados em um vetor:
predictions_slr <- predict(predictor,data_df)Regressão linear múltipla
Desta vez, começo considerando todas as variáveis no conjunto de dados ao prever o tamanho da população dos EUA:
# split data in training and test set
set.seed(123)
training_split <- sample.split(data_df$date, SplitRatio = 0.8)
training_df <- subset(data_df, training_split)
test_df <- subset(data_df, !training_split)
# train predictor with mutliple linear regression methodology, on training set
predictor <- lm(formula = population ~ gdp +
private_investment +
life_expectancy +
rnd, training_df)
# summarize regression outcome
summary(predictor)##
## Call:
## lm(formula = population ~ gdp + private_investment + life_expectancy +
## rnd, data = training_df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -10472.0 -1969.0 188.3 2421.8 7782.1
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -3.202e+05 4.488e+04 -7.133 1.07e-08 ***
## gdp 9.891e+00 2.970e+00 3.330 0.00184 **
## private_investment -3.272e+00 5.115e+00 -0.640 0.52598
## life_expectancy 7.283e+03 6.318e+02 11.527 1.93e-14 ***
## rnd -1.923e+02 8.065e+01 -2.385 0.02181 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3834 on 41 degrees of freedom
## Multiple R-squared: 0.9929, Adjusted R-squared: 0.9922
## F-statistic: 1440 on 4 and 41 DF, p-value: < 2.2e-16O R-quadrado ajustado melhorou em comparação com a regressão linear simples anterior. O volume de investimento privado não parece ser tão significativo na previsão do tamanho da população dos EUA. Portanto, aplico a eliminação de parâmetros passo a passo na qual elimino o volume de investimento privado como uma variável independente ao conduzir a análise de regressão:
# regression without private investment volume as independent variable
predictor <- lm(formula=population~gdp +
life_expectancy +
rnd, training_df)
# review model performance
summary(predictor)##
## Call:
## lm(formula = population ~ gdp + life_expectancy + rnd, data = training_df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -10412.6 -2275.0 247.7 2209.6 7794.9
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -3.225e+05 4.442e+04 -7.259 6.20e-09 ***
## gdp 8.598e+00 2.160e+00 3.980 0.000267 ***
## life_expectancy 7.316e+03 6.252e+02 11.702 8.41e-15 ***
## rnd -1.673e+02 7.006e+01 -2.388 0.021496 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3807 on 42 degrees of freedom
## Multiple R-squared: 0.9929, Adjusted R-squared: 0.9924
## F-statistic: 1948 on 3 and 42 DF, p-value: < 2.2e-16A eliminação do volume de investimento privado melhorou (ligeiramente) o R-quadrado ajustado. No entanto, ainda estou interessado em ver a distribuição dos resíduos.
Primeiro, um histograma de resíduos:
hist(predictor$residuals)
Em seguida, um gráfico qqnorm de resíduos:
qqnorm(predictor$residuals)
Agora avalio o desempenho do modelo prevendo os valores da população do conjunto de teste:
# predict test set population values
predictions <- predict(predictor,test_df)
# visualize model performance vs test set, along timeline
ggplot(test_df) +
geom_point(mapping=aes(x=date,y=population)) +
geom_line(mapping=aes(x=date,y=predictions),color="red") +
ggtitle("Multiple linear regression prediction of US population") +
xlab("Date") +
ylab("US population size [-]")
Antes de continuar com a regressão polinomial, armazeno previsões para todo o conjunto de dados em um vetor:
predictions_mlr <- predict(predictor,data_df)Regressão polinomial em R
Considerando o resultado da regressão linear múltipla após a eliminação retrógrada, parece que a expectativa de vida é bastante útil para prever o tamanho da população, afinal.
Portanto, tento conduzir a regressão polinomial em R, prevendo o tamanho da população dos EUA com conhecimento da expectativa de vida dos EUA ao nascer.
Minha abordagem é adicionar termos polinomiais, desde que isso melhore o R-quadrado ajustado:
# split in training and test set
set.seed(123)
training_split <- sample.split(data_df$date,SplitRatio = 0.8)
training_df <- subset(data_df, training_split)
test_df <- subset(data_df, !training_split)
# train predictor on first order term only, i.e. simple linear regression
predictor <- lm(formula = population ~ life_expectancy,training_df)
# review model performance
summary(predictor)##
## Call:
## lm(formula = population ~ life_expectancy, data = training_df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -15279 -6746 1131 4625 17762
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -840396.8 32055.5 -26.22 <2e-16 ***
## life_expectancy 14629.9 427.4 34.23 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 8377 on 44 degrees of freedom
## Multiple R-squared: 0.9638, Adjusted R-squared: 0.963
## F-statistic: 1172 on 1 and 44 DF, p-value: < 2.2e-16Agora me pergunto: posso melhorar o R-quadrado ajustado adicionando um termo polinomial de segundo grau? Deixa eu testar isso:
# polynomial two term regression
training_df$LE2 <- training_df$life_expectancy^2
predictor <- lm(formula = population ~ life_expectancy + LE2, training_df)
# review model performance
summary(predictor)##
## Call:
## lm(formula = population ~ life_expectancy + LE2, data = training_df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -10785.9 -4081.8 -715.1 4186.9 8913.4
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 4014088.8 604959.5 6.635 4.35e-08 ***
## life_expectancy -116186.0 16295.0 -7.130 8.34e-09 ***
## LE2 879.9 109.6 8.029 4.31e-10 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 5360 on 43 degrees of freedom
## Multiple R-squared: 0.9855, Adjusted R-squared: 0.9848
## F-statistic: 1463 on 2 and 43 DF, p-value: < 2.2e-16Sim. O R quadrado ajustado foi melhorado. O que acontece se eu adicionar um terceiro termo?
# polynomial three term regression
training_df$LE3 <- training_df$life_expectancy^3
predictor <- lm(formula = population ~ life_expectancy + LE2 + LE3, training_df)
# review model performance
summary(predictor)##
## Call:
## lm(formula = population ~ life_expectancy + LE2 + LE3, data = training_df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -10908 -3739 -862 4079 9125
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.196e+07 2.240e+07 0.534 0.596
## life_expectancy -4.367e+05 9.037e+05 -0.483 0.631
## LE2 5.187e+03 1.214e+04 0.427 0.671
## LE3 -1.927e+01 5.432e+01 -0.355 0.725
##
## Residual standard error: 5415 on 42 degrees of freedom
## Multiple R-squared: 0.9856, Adjusted R-squared: 0.9845
## F-statistic: 955.5 on 3 and 42 DF, p-value: < 2.2e-16Adicionar um terceiro termo não melhorou o R-quadrado ajustado. O que acontecerá se eu adicionar um quarto termo à regressão em R?
# polynomial four term regression
training_df$LE4 <- training_df$life_expectancy^4
predictor <- lm(formula = population ~ life_expectancy + LE2 + LE3 + LE4, training_df)
# review model performance
summary(predictor)##
## Call:
## lm(formula = population ~ life_expectancy + LE2 + LE3 + LE4,
## data = training_df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -11422.7 -2990.7 -4.8 2420.7 11496.0
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -2.345e+09 6.041e+08 -3.882 0.000369 ***
## life_expectancy 1.264e+08 3.250e+07 3.889 0.000362 ***
## LE2 -2.553e+06 6.555e+05 -3.895 0.000355 ***
## LE3 2.290e+04 5.873e+03 3.900 0.000350 ***
## LE4 -7.697e+01 1.972e+01 -3.903 0.000346 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 4680 on 41 degrees of freedom
## Multiple R-squared: 0.9895, Adjusted R-squared: 0.9884
## F-statistic: 963.4 on 4 and 41 DF, p-value: < 2.2e-16A adição de um quarto termo melhorou a regressão em R, pois o R-quadrado ajustado aumentou. Prossigo adicionando termos, adicionando um quinto e um sexto termo de regressão.
# polynomial six term regression
training_df$LE5 <- training_df$life_expectancy^5
training_df$LE6 <- training_df$life_expectancy^6
predictor <- lm(formula = population ~ life_expectancy + LE2 + LE3 +
LE4 + LE5 + LE6, training_df)
# review model performance
summary(predictor)##
## Call:
## lm(formula = population ~ life_expectancy + LE2 + LE3 + LE4 +
## LE5 + LE6, data = training_df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -12579.2 -2669.2 -306.2 1781.2 12719.2
##
## Coefficients: (1 not defined because of singularities)
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -3.842e+10 1.696e+10 -2.265 0.0290 *
## life_expectancy 2.459e+09 1.097e+09 2.243 0.0305 *
## LE2 -6.145e+07 2.768e+07 -2.220 0.0322 *
## LE3 7.276e+05 3.312e+05 2.197 0.0339 *
## LE4 -3.632e+03 1.671e+03 -2.174 0.0357 *
## LE5 NA NA NA NA
## LE6 4.285e-02 2.013e-02 2.128 0.0395 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 4491 on 40 degrees of freedom
## Multiple R-squared: 0.9905, Adjusted R-squared: 0.9894
## F-statistic: 837.9 on 5 and 40 DF, p-value: < 2.2e-16A adição de um quinto e sexto termo de regressão melhorou o R-quadrado ajustado. Decido continuar e adicionar um sétimo e um oitavo termo:
# polynomial seven term regression
training_df$LE7 <- training_df$life_expectancy^7
training_df$LE8 <- training_df$life_expectancy^8
predictor <- lm(formula = population ~ life_expectancy + LE2 + LE3 + LE4 +
LE5 + LE6 + LE7 + LE8, training_df)
# review model performance
summary(predictor)##
## Call:
## lm(formula = population ~ life_expectancy + LE2 + LE3 + LE4 +
## LE5 + LE6 + LE7 + LE8, data = training_df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -12579.2 -2669.2 -306.2 1781.2 12719.2
##
## Coefficients: (3 not defined because of singularities)
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -3.842e+10 1.696e+10 -2.265 0.0290 *
## life_expectancy 2.459e+09 1.097e+09 2.243 0.0305 *
## LE2 -6.145e+07 2.768e+07 -2.220 0.0322 *
## LE3 7.276e+05 3.312e+05 2.197 0.0339 *
## LE4 -3.632e+03 1.671e+03 -2.174 0.0357 *
## LE5 NA NA NA NA
## LE6 4.285e-02 2.013e-02 2.128 0.0395 *
## LE7 NA NA NA NA
## LE8 NA NA NA NA
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 4491 on 40 degrees of freedom
## Multiple R-squared: 0.9905, Adjusted R-squared: 0.9894
## F-statistic: 837.9 on 5 and 40 DF, p-value: < 2.2e-16O R-quadrado ajustado não melhorou. Eu decido parar a regressão polinomial aqui e visualizar o resultado da regressão:
ggplot(training_df) +
geom_point(mapping=aes(x=life_expectancy,y=population)) +
geom_line(mapping=aes(x=life_expectancy,y=predict(predictor,training_df)),
color="red") +
ggtitle("Trained polynomial regression model; degree 6") +
xlab("US life expectancy at birth [years]") +
ylab("US population size [-]")
Agora eu testo o modelo polinomial contra o conjunto de teste:
# add terms to test data frame
test_df$LE2 <- test_df$life_expectancy^2
test_df$LE3 <- test_df$life_expectancy^3
test_df$LE4 <- test_df$life_expectancy^4
test_df$LE5 <- test_df$life_expectancy^5
test_df$LE6 <- test_df$life_expectancy^6
test_df$LE7 <- test_df$life_expectancy^7
test_df$LE8 <- test_df$life_expectancy^8
# visualize predictor performance on test set
predictions <- predict(predictor,test_df)
ggplot(test_df) +
geom_point(mapping=aes(x=life_expectancy,y=population)) +
geom_line(mapping=aes(x=life_expectancy,y=predictions), color = "red") +
ggtitle("Polynomial regression on test data; degree 6") +
xlab("US life expectancy at birth [years]") +
ylab("US population size [-]")
Antes de passar para a regressão da árvore de decisão, armazeno previsões para todo o conjunto de dados em um vetor:
data_df$LE2 <- data_df$life_expectancy^2
data_df$LE3 <- data_df$life_expectancy^3
data_df$LE4 <- data_df$life_expectancy^4
data_df$LE5 <- data_df$life_expectancy^5
data_df$LE6 <- data_df$life_expectancy^6
data_df$LE7 <- data_df$life_expectancy^7
data_df$LE8 <- data_df$life_expectancy^8
predictions_poly <- predict(predictor,data_df)Regressão de árvore de decisão em R
Outra metodologia de regressão é a regressão de árvore de decisão. Nesse tipo de regressão, o espaço de soluções é dividido em subconjuntos, para os quais o valor médio de observação medido no conjunto de treinamento constitui uma predição.
Na seção abaixo, implemento a regressão da árvore de decisão em R:
# split in training and test set
set.seed(123)
training_split <- sample.split(data_df$date,SplitRatio = 0.8)
training_df <- subset(data_df, training_split)
test_df <- subset(data_df, !training_split)
# conduct decision tree regression
predictor <- rpart(formula = population ~ gdp +
private_investment +
life_expectancy +
population +
rnd,
data = training_df)
# generate predictions from test set
predictions <- predict(predictor,test_df)
residuals <- test_df$population - predictions
# visualize prediction accuracy along the timeline
ggplot(test_df) +
geom_point(mapping = aes(x=date,y=population)) +
geom_point(mapping = aes(x=date,y=predictions), color = "red") +
ggtitle("Decision tree regression performance on test set (red: predictions)") +
xlab("Date") +
ylab("US population size [-]")
Antes de passar para o suporte à regressão vetorial, armazeno minhas previsões para todo o conjunto de dados em outro vetor:
predictions_dtr <- predict(predictor,data_df)Suporta regressão vetorial
Eventualmente, eu conduzo a regressão do vetor de suporte. Eu apenas alimento as variáveis que a regressão linear múltipla descobriu serem estatisticamente significativas na previsão do tamanho da população dos EUA:
# split in training and test set
set.seed(123)
training_split <- sample.split(data_df$date,SplitRatio = 0.8)
training_df <- subset(data_df, training_split)
test_df <- subset(data_df, !training_split)
# construct predictor
predictor <- svm(formula = population ~ gdp +
life_expectancy +
rnd,
data = training_df,
type = "eps-regression")
# visualize prediction accuracy on test set along time line
ggplot(test_df) +
geom_point(mapping = aes(x=date, y = population)) +
geom_line(mapping = aes(x=date, y = predict(predictor,test_df)), color = "red") +
ggtitle("Support vector regression (eps methode) on test set") +
xlab("Date") +
ylab("US population size [-]")
Como nas outras partes da regressão, armazeno a previsão sobre todo o conjunto de dados como um espaço de solução em um vetor separado:
predictions_svr <- predict(predictor,data_df)Comparação das previsões do modelo
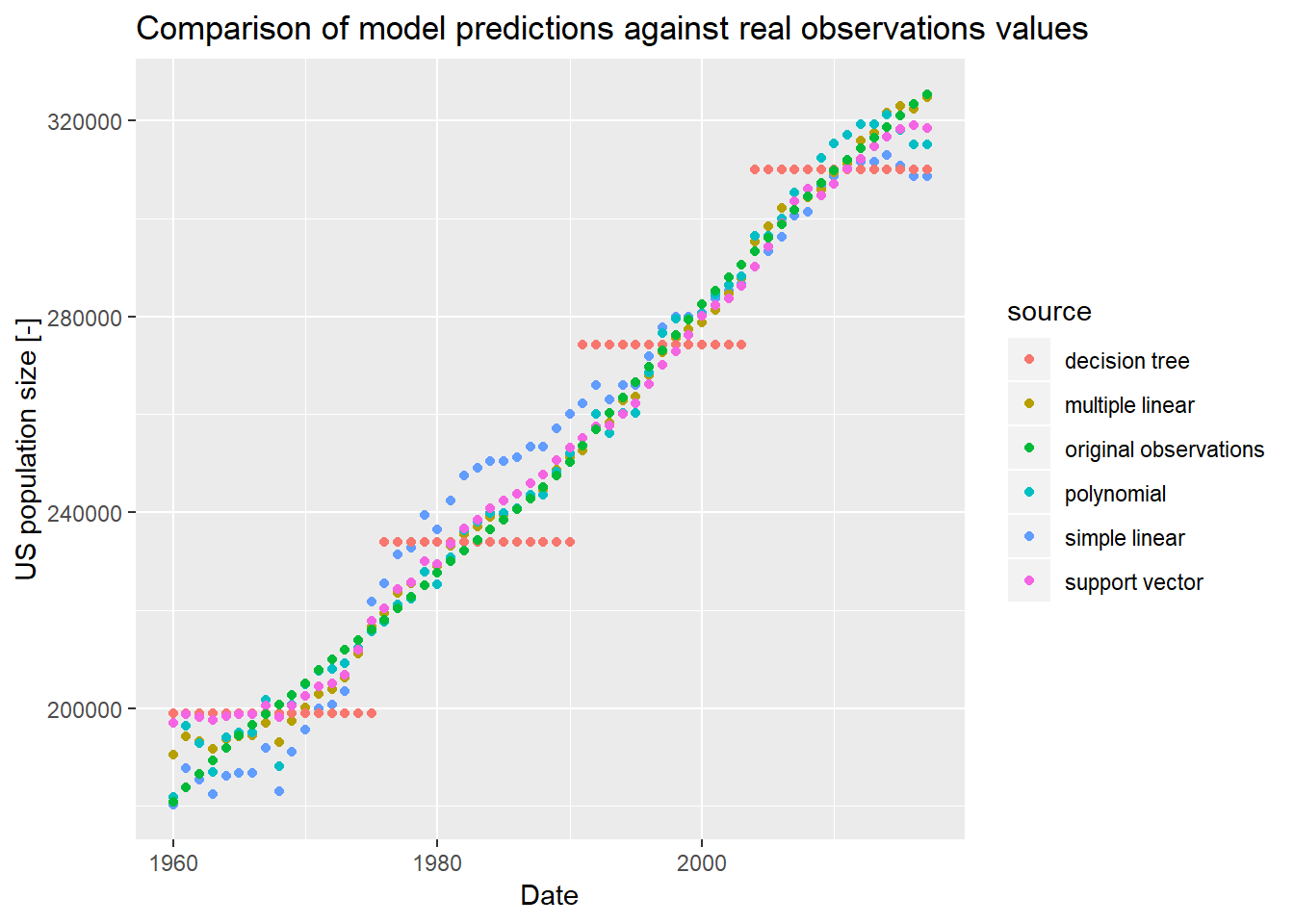
Usando os vetores com valores de previsões armazenados, podemos comparar os diferentes modelos de previsões na linha do tempo:
# construct ggplot friendly data frame
ggdata_df <- as.data.frame(matrix(nrow=nrow(data_df)*6,ncol=3))
colnames(ggdata_df) <- c("date","value","source")
ggdata_df$date <- rep(data_df$date,times=6)
ggdata_df$value <- c(predictions_slr,
predictions_mlr,
predictions_poly,
predictions_dtr,
predictions_svr,
data_df$population)
ggdata_df$source <- c(rep("simple linear", times=nrow(data_df)),
rep("multiple linear", times=nrow(data_df)),
rep("polynomial", times=nrow(data_df)),
rep("decision tree", times=nrow(data_df)),
rep("support vector", times=nrow(data_df)),
rep("original observations", times=nrow(data_df)))
# visualize
ggplot(ggdata_df) +
geom_point(mapping = aes(x=date, y=value, color=source)) +
ggtitle("Comparison of model predictions against real observations values") +
xlab("Date") +
ylab("US population size [-]")

Cientista de dados com foco em simulação, otimização e modelagem em R, SQL, VBA e Python

Leave a Reply