In this post I provide a coding example of how a group of customers can be assigned to one warehouse each, considering a set of fixed warehouses with unlimited capacity. The underlying assumption is that there are no fixed costs and that costs only depend on the euclidean distance between customer and warehouse. Furthermore, no lead time requirements or other service level related constrains are considered in this problem.

The algorithm is very simple and reminds one of clustering algorithms. It loops through all customers and assigns each customer to the closest warehouse, considering euclidean distance and the latitude-longitude system. Below I define this algorithm as a function:

# function for calculating euclidean distances
euclidean_distance <- function(vc,df){
  sqrt((as.numeric(rep(vc[1],times=nrow(df)))-df[,1])^2+(as.numeric(rep(vc[2],times=nrow(df)))-df[,2])^2)
}

# function for assigning customers to warehouses
assignment_algorithm <- function(customers,warehouses){
  return_df <- as.data.frame(matrix(nrow=nrow(customers),ncol=3))
  colnames(return_df)<-c("lat","long","warehouses")
  for(i in 1:nrow(customers)){
    return_df[i,] <- c(customers[i,1],customers[i,2],which.min(euclidean_distance(customers[i,],warehouses)))
  }
  return_df
}

To test I first build two sets, with randomly located customers and warehouses respectively.

customer_df <- as.data.frame(matrix(nrow=1000,ncol=2))
colnames(customer_df) <- c("lat","long")
warehouse_df <- as.data.frame(matrix(nrow=4,ncol=2))
colnames(warehouse_df) <- c("lat","long")

customer_df[,c(1,2)] <- cbind(runif(n=1000,min=-90,max=90),runif(n=1000,min=-180,max=180))
warehouse_df[,c(1,2)] <- cbind(runif(n=4,min=-90,max=90),runif(n=4,min=-180,max=180))

Below the header of the customer location dataframe:

head(customer_df)

##         lat      long
## 1 -35.42042 -33.68156
## 2 -50.63025 -64.52526
## 3  43.71663 -36.22302
## 4 -53.30511 135.56315
## 5 -46.32125  84.83210
## 6  83.85849 -60.70374

Below the header of the warehouse location dataframe:

head(warehouse_df)

##          lat      long
## 1 -41.007642  118.5673
## 2  81.968627  116.1495
## 3  11.971601  103.5034
## 4  -6.619224 -103.6206

Now I assign customers to warehouses:

# apply function
results_df <- assignment_algorithm(customer_df,warehouse_df)
# display header of result
head(results_df)

##         lat      long warehouses
## 1 -35.42042 -33.68156          4
## 2 -50.63025 -64.52526          4
## 3  43.71663 -36.22302          4
## 4 -53.30511 135.56315          1
## 5 -46.32125  84.83210          1
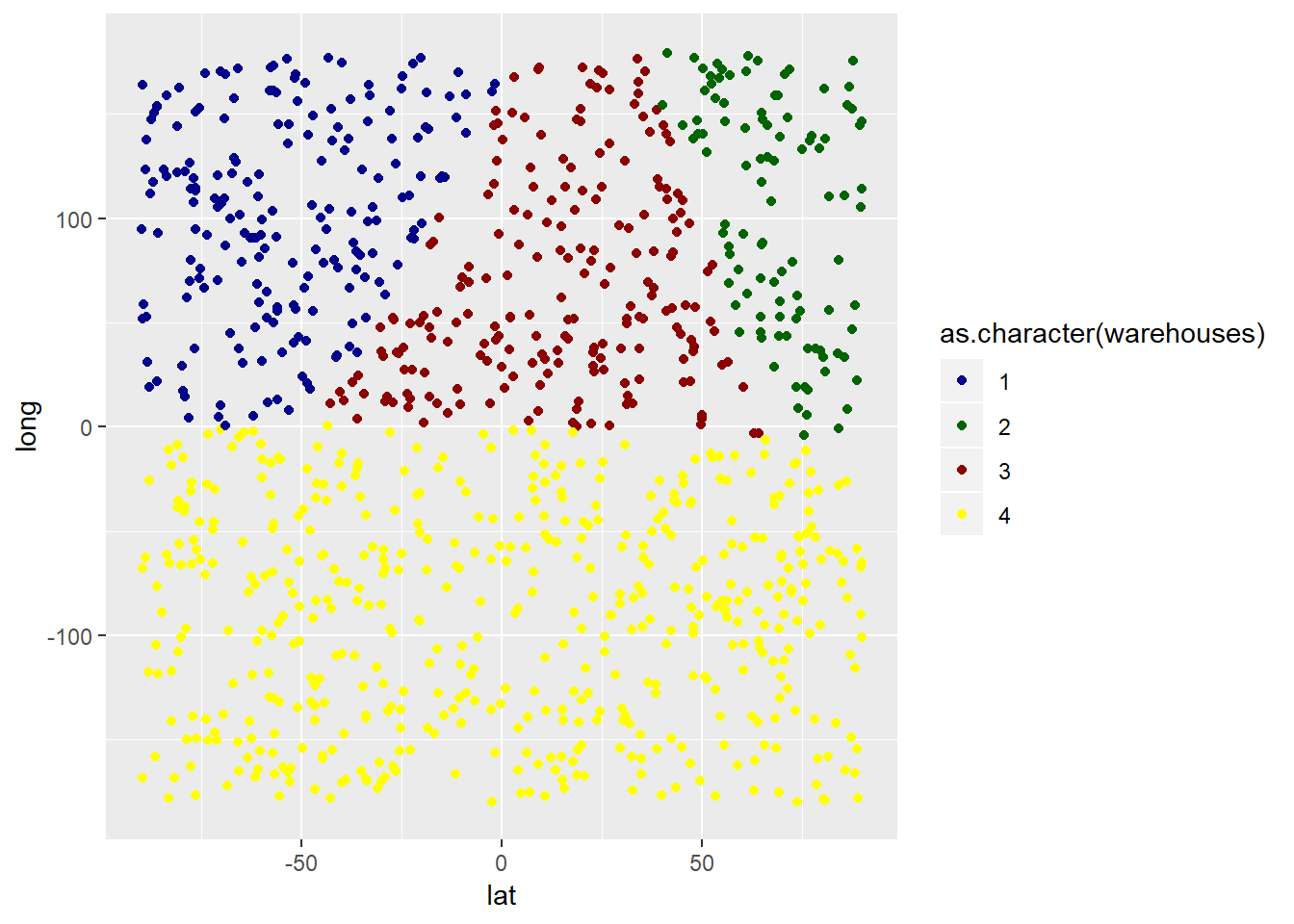
## 6  83.85849 -60.70374          4

In addition, I visualize the results in ggplot2:

library(ggplot2)
ggplot(data = results_df) + 
  geom_point(mapping = aes(x=lat,y=long,color=as.character(warehouses))) +
  scale_color_manual(values=c("darkblue","darkgreen","darkred","yellow")) +
  xlim(-90,90) + ylim(-180,180)

The warehouses are located as follows:

ggplot(data = warehouse_df) + geom_point(mapping = aes(x=lat,y=long)) + xlim(-90,90) + ylim(-180,180)

In another post I show how to locate a warehouse at the center of mass, I at the center of customer demand: Single warehouse problem – Locating warehouse at center of mass (center of mass calculation in R)

I have also written posts on how to divide a group of customers into several smaller clusters, based on spatial proximity. This approach can e.g. be used for locating multiple warehouses at each their center of mass in R.

Linnart Felkl

Data scientist focusing on simulation, optimization and modeling in R, SQL, VBA and Python